Ну скажем: тело бросили с начальной скоростью

под углом

к горизонту, вычислить длину траектории (=пройденный путь)
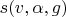
до падения на землю если ускорение свободного падения равно

, а сопротивление воздуха и прочие потери отсутствуют - можете?
А у Сивухина есть вычисление длины таких траекторий?
-- 08.08.2025, 18:28 --Как бы детски это ни звучало, я уже давно решил, что хочу работать над теорией всего, какой бы критики это всё ни подвергалась. Я не из тех, кто посмотрев пару научно-популярных видеороликов, вдруг решил посвятить этому всю жизнь. Нет. С малого возраста меня интересует природа мира и в итоге её целостность является смыслом моей жизни, как бы глупо это ни звучало от человека, пока ещё ничего не достигшего.
С одной стороны, тут присутствует юношеский максимализм.
С другой стороны, есть амбиции и целеустремленность, что уже хорошо.
Если декомпозировать Ваши задачи на относительно ближайшее будущее, то первой целью будет поступление в хороший университет с сильной кафедрой теоретической физики.
Соответственно, текущие усилия по образованию должны быть направлены на это.
Возможность что-то сделать значимое в современной физике, особенно в теор. физике, без соответствующего образования - миф. К сожалению.
-- 08.08.2025, 18:38 --Соответственно, текущие усилия по образованию должны быть направлены на это.
Кстати, может быть так, что не только по образованию.
Например, вместо самостоятельного изучения линала и-или матана на уровне 1-2 курса будет правильным зарабатывать деньги на обучение. Так тоже может быть, не знаю Вашу ситуацию.
-- 08.08.2025, 18:40 --Если не поступите, то вообще не сможете заниматься теоретической физикой.
плюс 100500