Та формула, это пространственная часть.
Почему система 1-го порядка?
Самосопряженность дифференциальных операторов обычно доказывают так:
1. Действуют дифференциальным оператором на функцию из области его определение, затем что получилось скалярно умножают на пробную функцию оттуда же, получается интеграл.
2. С помощью интегрирования по частям или формулы Грина-Остроградского-Гаусса перекидывают производные на пробную функцию.
3. При "хороших" граничных условиях внеинтегальный член обнуляется. Если дифференциальный оператор 2-го порядка и самосопряженный, то после двух таких действий он же будет действовать на пробную функцию.
4. Для дифференциальных операторов 1-го орядка, типа
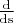
, самосопряженность не получится, поскольку при одном интегрировании по частям перед интегралом будет минус, т.е. сопряженный оператор будет равен минус исходному. Также, если краевые условия нехорошие, появится внеинтегральные члены, и самосопряженности тоже не получится.
5. В вашем случае возможно будет
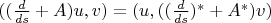
, где

- векторозначные функции, удовлетворяющие граничным условиям.
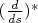
можно найти по указанному выше алгоритму.