Похоже, что обсуждение движется в никуда. Я постараюсь объяснить.
1. Формальный ОДО
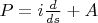
. Формальный потому, что область не обсуждается.
2. Сопряженный формальный ОДО:
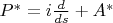
Я вставил множитель

, чтобы оператор можно было сделать самосопряженным.
Теперь начнем анализ:
3. Mаксимальный оператор: это формальный, но с областью
![$D(P_{max})=H^1([a,b]) = \{u, \frac{du}{ds} \in L^2([a,b])\}$ $D(P_{max})=H^1([a,b]) = \{u, \frac{du}{ds} \in L^2([a,b])\}$](https://dxdy-03.korotkov.co.uk/f/a/4/0/a40ce04883601bc853f4b7a6f7352bf182.png)
}.
4. Минимальный: это формальный, но с областью
![$D(P_{min})=H_0^1([a,b]) = \{u, \frac{du}{ds} \in L^2([a,b]), u(a)=u(b)=0\}$ $D(P_{min})=H_0^1([a,b]) = \{u, \frac{du}{ds} \in L^2([a,b]), u(a)=u(b)=0\}$](https://dxdy-03.korotkov.co.uk/f/2/f/5/2f5c996a1c2a75f64b4e57733f50b30682.png)
}.
Заметим, что
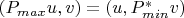
и наоборот; здесь каждый оператор может применяться только к функциям из своей области. Предположим, что формальный оператор симметричен:
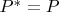
.
Тогда

симметричен
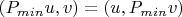
, но не самосопяжен, поскольку равенство это имеет место не только для
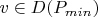
. Чтобы сделать оператор самосопряженным надо выбрать граничные условия так чтобы
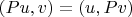
для всех
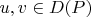
, причем если для какого-то

это верно для всех
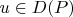
, то тогда
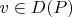
. Тогда автоматически если функции это вектор функции размерности

, то должно быть

граничных условий; если при этом каждое условие либо на левом, либо на правом конце, то на каждом конце д.б.

условий.
Пример

,
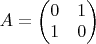
и условия
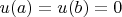
.
А вот если граничные условия путают концы, то это не так; пример

,
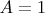
условия

.
В заключение: если даны два оператора, область первого меньше области второго, и на области первого они совпадают, то второй называется расширением первого. И по существу, мы обсуждали задачу: дан минимальный оператор, который симметричен, и мы хотим найти его самосопряженное расширение. В гораздо более общей постановке, чем сейчас, такое расширение может и не существовать.