Можно обобщить, задав функцию
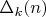
такую, что:
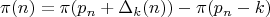
(LaTeX статья)
Код:
\documentclass[12pt]{article}
\usepackage{amsmath, amssymb, geometry, hyperref}
\usepackage{lmodern}
\usepackage[utf8]{inputenc}
\usepackage[russian]{babel}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{graphicx}
\usepackage{fourier}
\title{О функции $\Delta(n)$, отражающей симметричную плотность простых чисел}
\author{Jandos Mambetali}
\date{\today}
\begin{document}
\maketitle
\section*{Аннотация}
В данной заметке вводится и исследуется функция $\Delta(n)$, удовлетворяющая соотношению:
\[
\pi(n) = \pi(p_n + \Delta(n)) - \pi(p_n),
\]
где $p_n$ --- $n$-е простое число, а $\pi(x)$ --- функция распределения простых чисел. Мы предлагаем приближение:
\[
\boxed{
\Delta(n) \approx n \left(1 + \frac{\log\log n}{\log n} \right)
}
\]
и обсуждаем возможную научную ценность и направления обобщения.
\section{Введение}
Классические функции аналитической теории чисел, такие как функция распределения простых $\pi(n)$ и $n$-е простое число $p_n$, широко исследованы. Мы предлагаем новый способ их взаимосвязи, определяя функцию $\Delta(n)$ как длину интервала, следующего за $p_n$, в котором содержится столько же простых чисел, сколько в интервале от $1$ до $n$.
\section{Определение}
Определим $\Delta(n)$ следующим образом:
\begin{equation}
\pi(n) = \pi(p_n + \Delta(n)) - \pi(p_n)
\end{equation}
Иными словами, отрезок длиной $\Delta(n)$, начинающийся в точке $p_n$, содержит столько же простых чисел, сколько и отрезок от $1$ до $n$.
\section{Асимптотическая оценка}
Из аппроксимации $p_n \sim n \log n$ и $\pi(x) \sim \frac{x}{\log x}$ следует, что длина отрезка, содержащего $n$ простых чисел вблизи $p_n$, приближённо равна:
\begin{equation}
\Delta(n) \approx n \left(1 + \frac{\log\log n}{\log n} \right)
\end{equation}
Данная формула основана на плотности простых чисел в окрестности $p_n$ и поправке второго порядка.
\section{Численные примеры}
Для различных значений $n$ функция $\Delta(n)$ показывает хорошую сходимость:
\begin{itemize}
\item $n = 100$: $\Delta(100) \approx 100(1 + \frac{\log\log 100}{\log 100}) \approx 100(1 + \frac{\log 4.6}{\log 100})$
\item $n = 1000$: аналогично, оценка увеличивается логарифмически.
\end{itemize}
\section{Научная ценность и обобщения}
Предлагаемый подход представляет интерес, поскольку он предлагает новый способ сопоставления плотности простых чисел в разных участках числовой прямой. Это может быть полезно в исследованиях, связанных с равномерностью распределения простых, теоремой Бруна–Тичмарша и теорией интервалов с заданным числом простых.
Возможные направления дальнейших исследований:
Обобщением данной идеи является введение функции $\Delta_k(n)$, определяемой как длина интервала, следующего за $p_n$, содержащего $k$-кратное количество простых чисел по сравнению с интервалом $[1, n]$. То есть, пусть:
\[
\pi(p_n + \Delta_k(n)) - \pi(p_n) = k \cdot \pi(n)
\]
Тогда при $k = 1$ восстанавливается исходная функция $\Delta(n)$. Такое обобщение позволяет изучать поведение плотности простых на более длинных масштабах и может быть использовано для анализа кластеров простых чисел и их глобального распределения. Асимптотически можно ожидать:
\[
\Delta_k(n) \approx k \cdot n \left(1 + \frac{\log\log n}{\log n} \right)
\]
что требует дальнейшего теоретического обоснования и численного подтверждения.
\begin{itemize}
\item Обобщение $\Delta_k(n)$ с добавлением параметров;
\item Статистическое распределение $\Delta(n)$ при больших $n$;
\item Численные оценки и графики.
\end{itemize}
\section{Заключение}
Функция $\Delta(n)$ может стать новым инструментом в исследовании распределения простых чисел. Она отражает "симметрию" плотности простых относительно $n$ и $p_n$ и может иметь как теоретическую, так и прикладную ценность.
\end{document}