Пока остановлюсь здесь. Надо ещё полумать.
Подумал. Ниже напишу.
Если допустить, что

не делится на

, то

полный куб.
Если
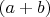
делится на

- согласно возражению
venco, тогда

делится на

и, соответственно,

делится на

. Как мне думается, условие делимости на

для

является проблемным. В смысле, если принять его, то можно получить противоречие. Которое говорит о том, что мы не должны его принимать.
Есть уравнение
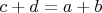
,

. Выше мной было показано, что

делится на

и, соответственно, на

, потому что может быть только чётным для любых случаев. Возводим в квадрат уравнение

и выражаем
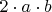
-слева, через остальные параметры-справа:
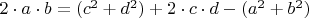
,

.
Слева:
слагаемое слева не делится на 
, т.к. нечётные

и

,
если оба не делятся на

, то не позволяют также иметь деление на любое число, кратное

. (Я понял возражение venco именно таким образом: если

делится на

, то ни

, ни

не делятся на

. Правильно ли я понял, или-нет, пусть эксперты судят.)
Справа:

делится на

, поскольку

делится на

, а значит, на

, т.к., является чётным.

делится на

, поскольку

делится на

, а значит, на

, т.к., является чётным.
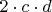
делится на

, т.к. мы нашли, что , и

, и

-оба-делятся на

.
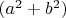
делится на

, поскольку это слагаемое раскладывается на два комплексных множителя, делящихся-каждый-на

, что даёт
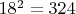
, которое кратно числу

.
Отсюда, вывод:

не делится на

.
Учитывая, что для

слагаемые легко переносятся вправо-влево, с сооответствующим переименованием параметров, когда

и

будут разной чётности, мы могли бы скаазать следом:
ВТФ (3) доказана.
Q.E.D.Проверьте-главное, что, если есть ошибка, то это была бы ошибка трансцендента, не резидента.  Ехал в машите-пришло в голову...Приехав, сразу набросал здесь этот текст.Не знаю-правильно или нет?
Ехал в машите-пришло в голову...Приехав, сразу набросал здесь этот текст.Не знаю-правильно или нет?Если допустить, что

делится на

, то

делится на

.
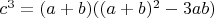
Предлагаю это пока отложить до времени, когда будет (или не будет?) обнаружена ошибка в моём тексте выше.
mihaild, пока не обнаружена ошибка в этом моём тексте , я думаю, Ваш вопрос пока не актуален:
transcendent в сообщении #1694531
писал(а):
Значит,

тоже делится на

Почему?
Согласны?
Что касается формулировки Леммы в другой моей ветке-я переформулирую её позже, когда будет время. Между "Пусть"("если") и "тогда" я вставлю МТФовские выражения, которые были обсуждены. Чтоб красиво было и по содержанию, и по форме, а в конце - проговорю о порядке, k. И дам Вам знать. Я хотел бы, чтобы Вы посмотрели текст Леммы и только после этого я начал бы редактирование текста доказательства. Его, действительно, можно сократить. Так нормально?