transcendent, что за хрень несете, причем постоянно. Остановитесь наконец!
Известно, что для минимального решения в натуральных чисел необходимо, чтобы : ровно одно из них делилось на

и ровно одно из них делилось на

. Вы хотите проверить случай, когда

исполняет обе эти обязательства. Хорошо. Тогда:
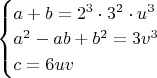
Просто, я хотел разобраться, как это у Вас получается число

под знаком радикала-число в квадрате,
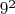
, чтобы получить делитель девятку,

, как итог, для

, если мы знаем такое тождество:
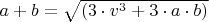
. При этом:

взаимнопростое с

, на

никаких ограничений не видно.
Если же мы будем писать, как это показано ниже, то я не увижу проблемы с наличием числа в квадрате, а именно

- под знаком радикала в упомянутом выше тождестве:
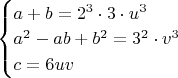
- Это при a и b, не являющихся взаимно простыми числами-напоминаю.
То, что

и
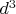
делятся на

и то, что там кубами можно выражать, дык это и до Вашего сообщения было известно.

Спасибо за искреннее желание помочь разобраться!
Но, пока Вы не убедили, что

делится на

. На

?-вижу, на

?-нет.
И почему в "последний раз"?
Хорошо, в последний раз объясняю вам вашу ошибку.
Впрочем, я ни на чём не настаиваю. Я уже писал:
мне больше нечего предложить здесь.
Пока-нечего. Может, Вы ещё чего-то предложите. Я не знаю...