Какое число показать?

[EUgeneUS]

mihaild в сообщении #1693281 писал(а):

ак проблема в зависимости $P$ и $Z$.

Посмотрим, что получается при $Q \equiv 1$

Выигрыш Боба: $B = Z (4P - 2P - 1)= Z (2P - 1)$
Матожидание выигрыша Боба: $E(B) = 2E(ZP) - E(Z)$
Да, так становится сложнее.
(удалил бред)

Для матожидания зависимых величин:
$E(ZP) = \operatoname{cov}(Z,P) - E(Z)E(P)$

Тогда матожидание выигрыша Боба: $E(B) = 2\operatoname{cov}(Z,P) - E(Z) (2E(P)-1)$

[EUgeneUS]

EUgeneUS в сообщении #1693286 писал(а):

Для матожидания зависимых величин:
$E(ZP) = \operatoname{cov}(Z,P) - E(Z)E(P)$

Тогда матожидание выигрыша Боба: $E(B) = 2\operatoname{cov}(Z,P) - E(Z) (2E(P)-1)$

$E(ZP) = \operatoname{cov}(Z,P) + E(Z)E(P)$
$E(B) = 2\operatoname{cov}(Z,P) - E(Z) (1-2E(P))$

[EUgeneUS]

1. Так как от $Q$ не зависят $P, Z$, а Боб может выбирать $Q$ случайно и независимо от $P, Z$, то выбирая свои ответы с вероятноcтью $0.5$ он может всегда "свести в ноль", независимо от стратегии Алисы.

2. Осталось найти стратегию Алисы, такую что Боб будет обязан свести игру "в ноль".

Провел небольшое моделирование Монте Карлом.
Если Боб всегда говорит "спрятанное число больше",
а) и Алиса выбирает, какое число спрятать с вероятностью $0.5$, то да, он выигрывает. Матожидание выигрыша где-то $0.15 ... 0.20$
б) Однако, если Алиса при этом прячет всегда меньшее число, то Боб проигрывает.

Это позволяет рассчитывать, что оптимальная стратегия Алисы описывается одним параметром: с какой вероятностью она прячет больше число.

[wrest]

EUgeneUS
У Алисы могут быть стратегии не только больше-меньше.
Можно же учитывать расстояние до середины. Или среднее. Или сумму. Или произведение. И т.п.
Есть например такая стратегия Алисы: если сумма меньше единицы, прятать меньшее. Если наоборот -- большее.

[worm2]

worm2 в сообщении #1693284 писал(а):

Если Алиса и Боб смотрят на числа, то, получается, стратегия Алисы — это функция двух переменных $f:[0,1]^2\to[0,1]$, а стратегия Боба — функция одной переменной $g:[0,1]\to[0,1]$.
И цена игры — это интеграл от хитрой комбинации этих функций. Причём при равновесии Нэша этот интеграл не должен зависеть ни от конкретной функции $f$ при оптимальной $g$, ни от конкретной функции $g$ при оптимальной $f$.
Как-то сложно. Я пока ниасилил.

Если всё-таки попробовать двигаться по этому пути, получается вот что.
Пусть $f(x,y)$ — вероятность того, что Алиса покажет $x$ (и спрячет $y$). Думаю, можно считать, что $f(x,y)=1-f(y,x)$.
$g(x)$ — вероятность того, что Боб скажет, что число $x$ — максимальное. Наверное, можно считать, что $g(0)=0$ и $g(1)=1$ (в принципе, любая $g$ в это ограничение "укладывается", так как одна точка всё равно ни на что не влияет, но мне это ограничение кажется естественным).
У нас два варианта для Алисы: A1 = "выбрать $x$ (спрятать $y$)" и A2 = "выбрать $y$ (спрятать $x$)".
И два варианта для Боба: B1 = "признать $x$ максимальным" и B2 = "признать спрятанное $y$ максимальным".
Цену игры $P$ будем считать для Алисы (для Боба она будет $-P$)
Вариант A1+B1 выпадает с вероятностью $f(x,y)g(x)$, его цена = $-y\operatorname{sgn}(x-y)$. Средняя цена такого исхода при фиксированных $x, y$ получается перемножением этих величин: $P(A1,B1,x,y)=-y\operatorname{sgn}(x-y)f(x,y)g(x)$.
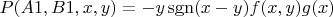
Вариант A1+B2 выпадает с вероятностью $f(x,y)(1-g(x))$, его цена = $+y\operatorname{sgn}(x-y)$. Средняя цена $P(A1,B2,x,y)=+y\operatorname{sgn}(x-y)f(x,y)(1-g(x))$.
Вариант A2+B1 выпадает с вероятностью $(1-f(x,y))g(y)$, его цена = $+x\operatorname{sgn}(x-y)$. Средняя цена $P(A2,B1,x,y)=+x\operatorname{sgn}(x-y)(1-f(x,y))g(x)$.
Наконец, вариант A2+B2 выпадает с вероятностью $(1-f(x,y))(1-g(y))$, его цена = $-x\operatorname{sgn}(x-y)$. Средняя цена $P(A2,B2,x,y)=-x\operatorname{sgn}(x-y)(1-f(x,y))(1-g(y))$.
Если генератор случайных чисел, выдающий исходные числа Алисе, будет всё время выдавать $x, y$, то Алиса в среднем будет выигрывать $P(x,y)=P(A1,B1,x,y)+P(A1,B2,x,y)+P(A2,B1,x,y)+P(A2,B2,x,y)$.
Средняя цена игры для Алисы по всем исходам $P[f;g]$ будет равна интегралу от $P(x,y)$ по квадрату $[0,1]^2$. Интеграл берётся с весом 1, потому что распределение равномерное (а то бы ещё на плотность вероятности нормировать пришлось).

$$\begin{align}P[f;g]=\int\limits_0^1\int\limits_0^1f(x,y)\left[x(1-2g(y))+y(1-2g(x))\right]\operatorname{sgn}(x-y)\,dx\,dy+\\ +\int\limits_0^1\int\limits_0^1 2g(y)x\operatorname{sgn}(x-y)\,dx\,dy+\int\limits_0^1\int\limits_0^1 -x\operatorname{sgn}(x-y)\,dx\,dy=I_1+I_2-\frac16\end{align}$$

$I_1$ зависит как от $f$, так и от $g$. $I_2$ зависит только от $g$.

Алисе нужно подобрать такую $f$, чтобы обеспечить себе максимальный выигрыш (минимальный проигрыш) при любом выборе $g$ Бобом (ей нужно оптимизировать только $I_1$, поскольку на $I_2$ она не имеет возможности повлиять). То же самое можно сказать про Боба (но он имеет влияние и на $I_1$, и на $I_2$). Напомню ограничения на $f$ и $g$: это функции, чьи аргументы меняются от 0 до 1, и значения тоже могут быть от 0 до 1, ибо это вероятности.

Что тут можно сказать? Наверное, такие штуки как-то решаются общими методами вариационного исчисления, но лично мои полномочия на этом всё. Я могу только, выбрав конкретное $f$ для Алисы, вычислить оптимальное $g$ для Боба или наоборот.

Например, если Алиса знает, что $g(x) \equiv x$, то ей нужно максимизировать

$$I_1=\int\limits_0^1\int\limits_0^1f(x,y)\left[x+y-4xy\right]\operatorname{sgn}(x-y)\,dx\,dy\to\max$$

Очевидно, этот максимум получится, если взять $f(x,y)=\theta(\operatorname{sgn}(x-y)(x+y-4xy))$, где $\theta$ — функция Хэвисайда, равная 0 при отрицательном аргументе и 1 при положительном. Таким образом, у Алисы получается чистая стратегия: если она видит, что $x+y>4xy$, то она выбирает наибольшее (и прячет наименьшее), если видит, что $x+y<4xy$, выбирает наименьшее.
Вычисления показывают, что при этом общая цена игры $P[f;g]$ получается равной $\frac{12+9\ln{3}}{576}\approx 0.038$ (численным экспериментом подтверждается).
Однако это далеко не точка равновесия Нэша. Зная, что Алиса выбирает такую стратегию, Боб может, например, всегда говорить "показано наименьшее число, спрятано наибольшее" ($g(x) \equiv 0$), что даёт ему выигрыш 0.18 (по результатам моделирования).

[Shadow]

Стратегия Боба более-менее ясна. Есть сакральное число $x$. Если Боб видит число больше $x$, говорит что спрятано меньшее число и наоборот.

Алиса знает стратегию Боба, более того ей известно число $x$. И рассуждает так:
1) Если оба числа больше $x$, я его обману и выигрыаю, причем большее из них.
2) Если оба числа меньше $x$, я его опять обману и выиграю меньшее из них.
3) Если одно больше, а другое меньше, то Боб выигрывает, причем меньшее их двух.

Вычисляю матожидания (возможно неправильно). $E=p_1E_1+p_2E_2-p_3E_3$. (Расчеты ссылаются на то, что при двух случайных чисел из $(0;1)$, матожидание меньшего - $1/3$, a большего - $2/3$)

$p_1=(1-x)^2,E_1=x+2/3(1-x)$

$p_2=x^2,E_2=x/3$

$p_3=2x(1-x),E_3=x/2$

Если не ошибся, то $E=1/3(5x^3-3x^2-3x+2)$

И Боб должен минимизировать данную функцию. $\min(E)=\dfrac{11-4 \sqrt 6}{25}$ при $x=\dfrac{1+\sqrt 6}{5}$

Приближенно: $E \approx 0.048$ при $x \approx 0.69$

Выигрыш у Алисы получается...

[EUgeneUS]

Shadow в сообщении #1693372 писал(а):

Стратегия Боба более-менее ясна. Есть сакральное число $x$. Если Боб видит число больше $x$, говорит что спрятано меньшее число и наоборот.

Это чистая стратегия. Сильно сомневаюсь, что тут есть равновесие в чистых стратегиях.

Shadow в сообщении #1693372 писал(а):

Выигрыш у Алисы получается...

Что в чистых стратегиях, что в смешанных, у Боба есть вариант инвертировать стратегию, при этом изменится знак выигрыша.
Поэтому Боб не может проиграть (при любой фиксированной стратегии Алисы).

-- 06.07.2025, 00:37 --

Опираясь на обозначения уважаемого worm2

Смешанная стратегия Боба: $g:[0,1]\to[0,1]$
Чистая стратегия Боба: $g:[0,1]\to \left\lbrace0,1\right\rbrace$

При $g(x) = 0.5$ Боб сводит в ничью при любой стратегии Алисы.

[EUgeneUS]

worm2 в сообщении #1693339 писал(а):

Пусть $f(x,y)$ — вероятность того, что Алиса покажет $x$ (и спрячет $y$).

Удобнее определить $f(x,y)$ — вероятность того, что Алиса покажет меньшее число, а спрячет бОльшее.
Тогда, $f(x,y) = f(y,x)$

1. Далее записываем интеграл, как у Вас. Вместо "сигнов" будут минимумы и максимумы.
2. Избавляемся от минимумов и максимумов, разбивая область интегрирования на области $x>y, x<y$.
3. Потом "пересобираем" интегралы.
4. И задаёмся вопросом, есть ли константа $p=f(x,y)$ такая, что интеграл становится нулём вне зависимости от
$g(x)$?
5. Если нигде не ошибся, то $p=0.25$

Итого:
вне зависимости от стратегии Боба, Алиса прячет бОльшее число с вероятностью $0.25$. Ничья.
вне зависимости от стратегии Алисы, Боб говорит "спрятано бОльшее число" с вероятностью $0.5$. Ничья.

[mihaild]

EUgeneUS в сообщении #1693389 писал(а):

Алиса прячет бОльшее число с вероятностью $0.25$.

Пусть Боб всегда говорит "спрятанное больше". Тогда на паре $x < y$ выигрыш Алисы равен $\frac{y - 3x}{4}$. Убирая положительные мультипликативные константы, получаем выигрыш Алисы

$$\int_0^1\, dx \int_x^1\, dy (y - 3x) = \int_0^1\, dx(1/2 - x^2 / 2 - 3x + 3x^2) = 1/2 - 1/6 - 3/2 + 1 = -1/6$$

.

[EUgeneUS]

Значит где-то ошибся в "пересборке" интегралов.

[EUgeneUS]

Запишу пока, что получилось.

Выигрыш Боба:

$$B = \int\limits_{[0,1]^2}^{} f(x,y) (2g(\max(x,y))-1) \max(x,y) + (f(x,y)-1) (2g(\min(x,y))-1) \min(x,y) \,dx \,dy $$

После избавления от минимумов и максимумов и перегруппировки, получается так:

$$\begin{align}B = \int\limits_{0}^{1} \int\limits_{0}^{1} f(x,y) (2g(x)-1) x \,dx \,dy + \int\limits_{0}^{1} \int\limits_{0}^{1} f(x,y) (2g(y)-1) y \,dx \,dy - \\ -\int\limits_{0}^{1} \,dy \int\limits_{y}^{1} \,dx (2g(y)-1) y - \int\limits_{0}^{1} \,dy \int\limits_{0}^{y} \,dx (2g(x)-1) x \end{align}$$

-- 06.07.2025, 05:54 --

Рассмотрим случай
а) $ f(x,y) = f(y,x)$ (Алиса не нумерует ГСЧ)
б) $g(x) = q$ - константа. Боб не смотрит на показанное число.
в) но тогда можно поискать $ f(x,y) = p$ - константа

Тогда можно переписать так:

$$\begin{align}B = (2q-1) \left ( 2 p \int\limits_{0}^{1} \int\limits_{0}^{1} x \,dx \,dy - \int\limits_{0}^{1} \,dy \int\limits_{y}^{1} y \,dx - \int\limits_{0}^{1} \,dy \int\limits_{0}^{y} x \,dx \right ) \end{align}$$

Легко видеть, что если в больших скобках не ноль, то Боб максимизирует свой выигрыш, выбирая одну из крайних стратегий. Поэтому в больших скобках должен быть ноль.

-- 06.07.2025, 06:00 --

Посчитаем

$$2p \cdot \frac{1}{2} = p = \int\limits_{0}^{1} (y(1-y) + \frac{y^2}{2}) \,d y = \int\limits_{0}^{1} (y - \frac{y^2}{2}) \,d y = \frac{1}{2} - \frac{1}{6} = \frac{1}{3}$$

-- 06.07.2025, 06:01 --

Понятно, что случай $g(x)$ - не константа, остался не рассмотренным

[Shadow]

EUgeneUS в сообщении #1693384 писал(а):

Это чистая стратегия. Сильно сомневаюсь, что тут есть равновесие в чистых стратегиях.

А я проверил может ли Боб улучшить свое положение, зная стратегию Алисс. Оказывается - нет, себе дороже. И настаиваю, что выигрыш у Алисы.
И так я-Алиса. И я вам говорю свою стратегию:

Есть константа $c=\dfrac{1+\sqrt 6}{5}$

Если оба числа больше $c$, то я вам показываю меньшее.
Если оба числа меньше $c$, то я показываю большее.
Если одно больше, а друго меньше $c$, то я показываю большее.

Вот и постройте вашу(Боба) стратегию, исходя из этой информации. Посмотрим что получится.

[EUgeneUS]

Shadow в сообщении #1693398 писал(а):

Вот и постройте вашу(Боба) стратегию, исходя из этой информации.

Построено уже всё.
Вот это построено без дополнительных предположений о $f(x,y)$ и $g(x)$

$$\begin{align}B = \int\limits_{0}^{1} \int\limits_{0}^{1} f(x,y) (2g(x)-1) x \,dx \,dy + \int\limits_{0}^{1} \int\limits_{0}^{1} f(x,y) (2g(y)-1) y \,dx \,dy - \\ -\int\limits_{0}^{1} \,dy \int\limits_{y}^{1} \,dx (2g(y)-1) y - \int\limits_{0}^{1} \,dy \int\limits_{0}^{y} \,dx (2g(x)-1) x \end{align}$$

Ваша функция Алисы удовлетворяет условию $f(x,y) = f(y,x)$
При фиксированной стратегии Алисы. Буду искать функцию Боба, как константу. То есть Боб не глядит на показанное число, а с некоторой вероятностью $q$ заявляет, что спрятано бОльшее число, а с вероятностью $1-q$, что спрятано меньшее число.

Тогда это перепишется так:

$$\begin{align}B = (2q-1) \left ( 2 \int\limits_{0}^{1} \int\limits_{0}^{1} f(x, y)x \,dx \,dy - \int\limits_{0}^{1} \,dy \int\limits_{y}^{1} y \,dx - \int\limits_{0}^{1} \,dy \int\limits_{0}^{y} x \,dx \right ) \end{align}$$

Совершенно очевидно, что если в больших скобках не ноль, то Боб
а) Обеспечивает себе выигрыш. Так как может изменить знак результата "инверсией стратегии" $q \to 1-q$
б) Максимум выигрыша Боба будет в одной из крайних стратегий: либо $q=0$ (Боб всегда говорит "спрятано меньшее число"), либо $q=1$ (Боб всегда говорит "спрятано большее число")

-- 06.07.2025, 09:33 --

Можно и по-другому показать.
Легко видеть, что при инверсии стратегии Боба $g(x) \to 1 - g(x)$, агрегат $2g(x)-1$ сохраняет модуль, но меняет знак.

Поэтому я утверждаю, что при фиксированной стратегии Алисы,
если Боб делал вот так:

Shadow в сообщении #1693372 писал(а):

Есть сакральное число $x$. Если Боб видит число больше $x$, говорит что спрятано меньшее число и наоборот.

и проиграывал:

Shadow в сообщении #1693372 писал(а):

Приближенно: $E \approx 0.048$

то при вот такой стратегии: если Боб видит число больше $x$, говорит что спрятано большее число и наоборот - Боб будет выигрывать ровно столько же.

[Shadow]

EUgeneUS в сообщении #1693401 писал(а):

При фиксированной стратегии Алисы. Буду искать функцию Боба, как константу. То есть Боб не глядит на показанное число, а с некоторой вероятностью $q$ заявляет, что спрятано бОльшее число, а с вероятностью $1-q$, что спрятано меньшее число.

Дайте значение $q$, сделаю симуляцию.

[EUgeneUS]

Shadow в сообщении #1693405 писал(а):

Дайте значение $q$, сделаю симуляцию.

$q=1$ и $q=0$
Утверждаю, что значения по модулю будут одинаковыми, но разными по знаку.

-- 06.07.2025, 10:04 --

BTW, можно ещё проще показать, если вернуться к записям через случайные величины.

EUgeneUS в сообщении #1693271 писал(а):

$B = Z (PQ + (1-P)(1-Q)) - Z(Q(1-P) + P(1-Q)) = Z (4PQ - 2P - 2Q +1)$

$P$ - случайная величина, принимающее значение $1$, если Алиса спрятала большее число и $0$ в противном случае.
$Q$ - случайная величина, принимающее значение $1$, если Боб сказал "спрятано большее число" и $0$ в противном случае.
$Z$ - случайная величина, равная спрятанному числу.
$B$ - здесь случайная величина, равная выигрышу Боба.

Перепишем так:$B = Z(2P-1)(2Q-1)$

От $Q$ никакие другие величины не зависят - Боб делает ход последним. Теперь пусть и $Q$ ни от чего не зависит - Боб не смотрит на показанное число. Тогда матожидания:

$$E\left [ B \right ] = E\left [ Z(2P-1)(2Q-1) \right ] = E\left [ Z(2P-1) \right ] E\left [ (2Q-1) \right ] = (2q-1) E\left [ Z(2P-1) \right ]$$

И вывод тот же самый: Боб максимизирует свой выигрыш в одной из крайних стратегий, если $E\left [ Z(2P-1) \right ] \ne 0$