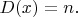Если я правильно поняла прочитанное о кольцах дискретного нормирования, то в моем случае дискретное нормирование на римановой поверхности

- это сопоставление каждой функции из поля мероморфных функций на

ее порядка в некоторой точке

Поскольку для голоморфных функций эти порядки неотрицательны, то

действительно является кольцом дискретного нормирования.
Равенство

мне, кажется, тоже интуитивно понятно: если на открытом множестве

мы имеем
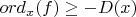
для всех

то это неравенство равносильно неравенству

т.е. то, что стоит с левой стороны - "голоморфная" функция на

Наверное, главное, в чем я плаваю: почему мы пишем, что

- кольцо (модуль?) ростков мероморфных функций, имеющих в точке

порядок "не выше"

а в равенстве

берем "ровно"

Не знаю, как точнее поставить вопрос.
В любом случае из равенства

Не совсем понимаю, как из последнего равенства сделать вывод, что

Если я еще окончательно не запуталась, то