Для чего нужны комплексные числа?

[katzenelenbogen]

Для чего нужно пространство комплексных чисел?

Почему не хватает плоскости $\mathbb{R}^2$?
Понятно, что комплексную плоскость отличает от плоскости $\mathbb{R}^2$ наличие операции умножения двух векторов, и в $\mathbb{R}^2$ её нет, но неужели просто в $\mathbb{R}^2$ нельзя ввести отдельную операцию, назвав её по-другому, такого же умножения двух векторов, и оставаться дальше в теории и во всём только в ней?

Прошу посмотреть на вопрос в том аспекте, в котором описал его я, а не давая стандартных и общеизвестных ответов из учебников и из всего остального наподобие "комплексные числа нужны для того, чтобы алгебраические уравнения всегда решались".

[Утундрий]

katzenelenbogen в сообщении #1664819 писал(а):

неужели просто в $\mathbb{R}^2$ нельзя ввести отдельную операцию, назвав её по-другому, такого же умножения двух векторов, и оставаться дальше в теории и во всём только в ней?

Вы хотите ввести комплексные числа, только не называть их комплексными числами. У вас комплексночислобоязнь?

[Anton_Peplov]

katzenelenbogen в сообщении #1664819 писал(а):

но неужели просто в $\mathbb{R}^2$ нельзя ввести отдельную операцию, назвав её по-другому, такого же умножения двух векторов, и оставаться дальше в теории и во всём только в ней?

Анализ на $\mathbb R^2$ (функции двух действительных переменных) и анализ на $\mathbb C$ (функции одной комплескной переменной) - это существенно разные области математики с разными теоремами. Иначе говоря, обобщение понятий из одномерного анализа (непрерывность, дифференцируемость и т.д.) на эти два случая приводит к разным результатам. Например, функция $\mathbb C \to \mathbb C$, дифференцируемая в некоторой области, имеет в этой области производные всех порядков и разлагается в ряд Тейлора. Для функции двух действительных переменных это не так.

Обе эти области математики нужны, ни одну из них не выбросишь. Поэтому $\mathbb R^2$ без умножения векторов и $\mathbb R^2$ с умножением векторов нужно называть по-разному. Исторически сложилось так, что $\mathbb R^2$ с умножением векторов называют комплексными числами. Можно переименовать в какие-нибудь сепульки, но отличать от $\mathbb R^2$ без умножения векторов все равно придется.

[Geen]

https://youtu.be/r5mccK8mNw8 (Michael Penn)
Краткое резюме - "двумерное поле" только одно, и это комплексные числа.

[Anton_Peplov]

Geen в сообщении #1664855 писал(а):

Краткое резюме - "двумерное поле" только одно, и это комплексные числа.

О, тут все еще интереснее.

Slav-27 в сообщении #1562408 писал(а):

$\mathbb R$ и $\mathbb C$ -- это единственные полные связные локально компактные хаусдорфовы топологические поля. (Понятие полноты имеет смысл для любой топологической абелевой группы, определяется как обычно через последовательности Коши.)

Это следствие 3 фактов:

• Топология любого локально компактного хаусдорфова топологического поля индуцируется некоторым вещественнозначным нормированием (Warner, Topological rings, теорема 16.3).
• Любое ультраметрическое пространство (это где усиленное неравенство треугольника вместо обычного) вполне несвязно; в частности, любое поле с топологией, индуцированной неархимедовым нормированием.
• Любое поле, полное относительно (вещественнозначного) архимедова нормирования, изоморфно $\mathbb R$ или $\mathbb C$ как топологическое поле -- теорема Островского (одна из).

UPD. Это верно даже если не требовать полноты (Понтрягин, Непрерывные группы, § 27).

Добавлю от себя: $\mathbb C$ - единственное поле конечной размерности, включающее $\mathbb R$ как собственное подмножество.

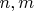
Но, как я понял, ТС спрашивает не зачем нам нужно $\mathbb C$ (которое $\mathbb R^2$ с умножением векторов), а зачем нам нужно $\mathbb R^2$ без умножения векторов. А вот нужно. В учебнике матанализа Зорича излагается анализ для функций $\mathbb R^m \to \mathbb R^n$, с произвольными конечными $n, m$ и без умножения векторов. А потом из этого корня вырастает анализ на многообразиях, дифференциальная геометрия и куча других вещей, которые не вырастишь из ТФКП.

[drzewo]

Anton_Peplov в сообщении #1664859 писал(а):

О, тут все еще интереснее.

Это действительно все очень интересно. Только, когда люи обнаружили комплексные числа, они ничего этого не знали, они поняли другое: с помощью комплексных чисел решаются задачи, которые ранее ни хрена не решались. Кватернионы -- тоже любопытная штука. Только они практически бесполезны. То, что можно сделать с ними -- можно также хорошо сделать и без них.

[mihaild]

По-моему, всё правильно сказал Утундрий, а вот рассуждения о достоинствах комплексных чисел тут уже лишнее.

katzenelenbogen в сообщении #1664819 писал(а):

но неужели просто в $\mathbb{R}^2$ нельзя ввести отдельную операцию, назвав её по-другому, такого же умножения двух векторов, и оставаться дальше в теории и во всём только в ней?

Можно. Можно даже вещественные числа не вводить, а работать с классами эквивалентностей последовательностей классов эквивалентности пар классов эквивалентностей пар натуральных чисел. Но смысла нет.
Про комплексные числа можно сказать столько всего без разбора их на действительную и мнимую части, что имеет оказывается удобно ввести обозначения, в которых эти части являются вторичными по отношению к самому числу.

[Geen]

Anton_Peplov в сообщении #1664859 писал(а):

О, тут все еще интереснее.

Ой, интересного там железнодорожный состав и маленькая тележка. Я просто не слишком длинное видео "подыскал". (думаю, если бы Slav-27 решился бы записать аналогичное видео (я бы, кстати, с удовольствием посмотрел), то оно бы часа на 4 с лишним получилось бы )

[Anton_Peplov]

drzewo в сообщении #1664864 писал(а):

Только, когда люди обнаружили комплексные числа, они ничего этого не знали, они поняли другое: с помощью комплексных чисел решаются задачи, которые ранее ни хрена не решались.

Разумеется. Однако, по-моему, несмотря на неудачный заголовок темы, ТС и не отрицает полезность комплексных чисел. Он спрашивает другое: если комплексное число - это пара действительных, и сложение там как в $\mathbb R^2$, почему бы не ввести "комплексное" умножение и деление прямо в $\mathbb R^2$? Зачем нужно сохранять линейное пространство $\mathbb R^2$, не являющееся полем, а для поля придумывать отдельное обозначение $\mathbb C$?

В этом отношении сообщение Geen (и мое к нему дополнение) не отвечает на вопрос ТС. А на вопрос ТС я попытался ответить здесь:

Anton_Peplov в сообщении #1664850 писал(а):

Анализ на $\mathbb R^2$ (функции двух действительных переменных) и анализ на $\mathbb C$ (функции одной комплескной переменной) - это существенно разные области математики с разными теоремами.

[мат-ламер]

katzenelenbogen в сообщении #1664819 писал(а):

Для чего нужно пространство комплексных чисел?

Почему не хватает плоскости $\mathbb{R}^2$?

Кроме всего прочего, математика это ещё и специальный язык, придуманный для удобства.

[Anton_Peplov]

Давайте действительно дождемся комментариев или уточняющих вопросов от ТС. Кажется, все, что можно было сказать в ответ на стартовое сообщение, уже сказано.

[katzenelenbogen]

Честно говоря, я не понимаю, для чего нужны объекты $a+bi$. Несмотря на то, что я помню определение, операции, формулы и т.д. и неоднократно сдавал это без проблем на отлично. Совершенно непонятные объекты. Понятно, для чего нужны обычные числа - для выражения количества, и совсем непонятно, что могло бы значить, когда прибавляется ещё мнимая часть. Вот объём какого-нибудь вещества - это обычные числа, а как представить себе "объём какого-то вещества с дополнительной мнимой частью", как её увидеть?

[EUgeneUS]

drzewo в сообщении #1664864 писал(а):

Кватернионы -- тоже любопытная штука. Только они практически бесполезны. То, что можно сделать с ними -- можно также хорошо сделать и без них.

Удивительный факт относительно недавно узнал. Сначала было слово были кватернионы, а потом от них оторвали действительную часть, и получились векторы.

(как я узнал про кватернионы)

В 80-х годах прошлого века приехал в ЛШ. Там были лекции по физике и математике.
По физике набор лекций был на тему "Как решать задачи по физике"
А по математике был курс про кватернионы. На полном серьезе. Лектор выходил и рассказывал, что такое кватернионы и доказывал теорем(ы\у) Вейерштрасса для них. Целый месяц.

Потом, спустя годы, узнал, почему так произошло
Но было много забавного, в том числе и забавных наблюдений за людьми

-- 13.12.2024, 19:03 --

katzenelenbogen
Поймите один простой факт. Для погроммистов.
Комплексные числа - это некий класс объектов.
А векторы в 2D с операцией умножения или объекты вида $a+bi$ - это всего лишь представления, реализации объектов этого класса.

[Anton_Peplov]

katzenelenbogen
Какой факультет Вы заканчивали?

[drzewo]

katzenelenbogen в сообщении #1664941 писал(а):

Честно говоря, я не понимаю, для чего нужны объекты $a+bi$. Несмотря на то, что я помню определение, операции, формулы и т.д. и неоднократно сдавал это без проблем на отлично. Совершенно непонятные объекты. Понятно, для чего нужны обычные числа - для выражения количества, и совсем непонятно, что могло бы значить, когда прибавляется ещё мнимая часть. Вот объём какого-нибудь вещества - это обычные числа, а как представить себе "объём какого-то вещества с дополнительной мнимой частью", как её увидеть?

Посмотрите книжку <<Методы ТФКП>> Лаврентьев Шабат. Там содержится много приложений к физике.