Необходимость производной и понимание её полезности

[miflin]

Чудны дела твои, господи...
Простые (нуачо, без производных же! ) школьно-оптические методы (не к ночи будь помянуты)
отобьют, надеюсь, нежелание изучать производные. Меньше головной боли.

[drzewo]

(Оффтоп)

воображаю как ТС угорает с этой ветки

[sergey zhukov]

Вот одна из интересных практических задач, где помогает производная.

Через пропасть шириной $l$ требуется перебросить канатный мост. Какую длину подвесного троса моста $s$ следует взять, чтобы максимальное натяжение в этом подвесном тросе (это в точках его крепления) было наименьшим?
Ясно, что слишком короткий трос сильно натягивается, т.к. сила натяжения становится близкой к горизонтальной. Слишком длинный трос так же сильно натягивается из-за большого веса. Где-то есть минимум натяжения.

Примем, что мост - это просто трос (цепь) с линейной плотностью $\gamma$. Уравнение цепной линии:

$$y=\frac{a}{2}(e^{\frac{x}{a}}+e^{\frac{-x}{a}})$$

Известно, что параметр $a$ имеет смысл отношения горизонтальной компоненты силы растяжения цепи к погонному весу цепи, т.е.:

$$a=\frac{F_{hor}}{g\gamma}$$

Высота точек подвеса, на которой расстояние между ними будет равно $l$ есть:

$$y_l=\frac{a}{2}(e^{\frac{l}{2a}}+e^{\frac{-l}{2a}})$$

Известно, что длина цепной линии от нижней точки провиса до точки крепления есть:

$$s_{\frac{1}{2}}=\sqrt{y_l^2-a^2}$$

Тогда вес половины цепи (который равен вертикальной составляющей силы натяжения в точке подвеса) есть:

$$F_{vert}=\gamma g \sqrt{y_l^2-a^2}$$

Тогда сила натяжения цепи в точках подвеса есть:

$$F=\sqrt{F_{hor}^2+F_{vert}^2}=\gamma g y_l=\frac{\gamma g a}{2}(e^{\frac{l}{2a}}+e^{\frac{-l}{2a}})$$

Минимум силы натяжения имеем при условии $F^\prime_a=0$, т.е:

$$\frac{\gamma g}{2}(e^{\frac{l}{2a}}+e^{\frac{-l}{2a}}+\frac{l}{2a}(e^{\frac{-l}{2a}}-e^{\frac{l}{2a}}))=0$$

Если обозначить $z=\frac{l}{2a}$, то:

$$e^{z}+e^{-z}+z(e^{-z}-e^{z})=0$$

Высота подвеса будет равна:

$$y_l=\frac{l}{4z}(e^z+e^{-z})$$

И длина всей цепи будет равна:

$$s=2\sqrt{y_l^2-a^2}=\frac{l}{z}\sqrt{\frac{1}{4}(e^z+e^{-z})^2-1}$$

Численное решение уравнения для $z$ дает $z=1,996$

Тогда

$$s=1,2577l$$

Т.е. для минимального натяжения троса нужно взять его примерно на четверть длиннее, чем ширина пропасти.
Интересно, что угол натяжения такого троса (в точке подвеса относительно горизонта) будет очень близок к 1 радиану, но все же не равен ему (он равен 0,985 рад).

Вот как выглядит подвес с минимальным натяжением в точках подвеса, а так же зависимость этого натяжения от отношения $\frac{s}{l}$:


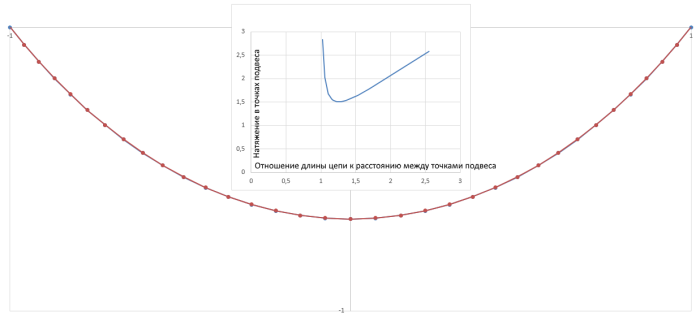
Пожалуй, это слишком круто для подвесного моста.

[Утундрий]

sergey zhukov в сообщении #1658669 писал(а):

Вот одна из интересных практических задач, где помогает производная

Но все рекорды полезности и интересности бьёт следующая задача: Вычислите производную функции...