Допустим вы можете с вероятностью
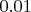
выиграть миллиард, или остаться ни с чем. В другой страте вам точно дадут миллион. Матожижание первой стратегии больше, но логично выбрать вторую
Для простоты предположим, что случайные величины

имеют одинаковый закон распределения (для определенности нормальный), но с разными параметрами.
Исходя из этого, попытайтесь ответить на два вопроса:
1. Если

- какую случайную величину следует выбрать для "обогащения".
2. Если

- какую случайную величину следует выбрать для "обогащения".
Чему соответствуют эти два случая для вашего критерия?