Разбрызгиватель Фейнмана.

[chislo_avogadro]

Утундрий в сообщении #1576031 писал(а):

chislo_avogadro в сообщении #1576027 писал(а):

В то же время уравнение Эйлера

Выше я намекнул (да что там, прямо заявил), что Эйлер нам тут не товарищ.

Верно, следовало это упомянуть. Моё слабое оправдание вижу в подаче Эйлера у меня и у вас под разными соусами - вы от него шли в направлении Навье-Стокса, я же склоняюсь к Ньютону, и асимметрию вижу в граничных условиях, т.е. в конкретной конструкции "установки". Возможно, slavav это и имел ввиду, говоря о несимметричности гидродинамики. И если в его модификации опыта - лодка плюс труба в виде колена - жидкость заменить биллиардным шаром, то анализировать, как мне кажется, становится проще: втягиваемый в горизонтальную часть трубы шар при повороте обнуляет приобретённый ею импульс.

[Утундрий]

sergey zhukov в сообщении #1576154 писал(а):

поле скоростей и давлений будет совершенно одинаковым независимо от вязкости жидкости, даже если она равна нулю?

Нет, по крайней мере давление зависит от вязкости.

[EUgeneUS]

slavav в сообщении #1576033 писал(а):

Надо рассматривать всю историю порции воды. До того как шар подплыл к порции она была неподвижна.

IMHO, на рассматривать не историю, а систему.
А для этого систему нужно определить. Например, замкнутой линией, границей, нарисованной фломастером на чертеже.

[sergey zhukov]

Утундрий
Интересно.

Я взял Гидродинамику ЛЛ, уравнение Навье-Стокса в цилиндрических координатах (15.18) для стационарного плоского случая $\frac{\partial}{\partial t}=0$ и $\frac{\partial}{\partial z}=0$, подставил туда $u_r=\frac{1}{r}$ согласно уравнению неразрывности для радиального потока и получил, что член с вязкостью исчезает и решение совпадает с решением для идеальной жидкости. Вязкость в окончательный ответ не вошла.

Вроде бы чушь, но ошибки вроде нет.

[Утундрий]

sergey zhukov
Тогда, пока ешё держите ЛЛ6 в руках, долистайте до формулы $(23,8)$, где вязкость определённо есть.

[sergey zhukov]

Утундрий в сообщении #1576202 писал(а):

формулы $(23,8)$

Ну так стенки же здесь, условие прилипания. Тут трение ожидается. Тут же не просто сектор радиального течения из предыдущей задачи.

[Утундрий]

Согласен, задачи разные. Если просто кусок радиального течения, то да - вязкость сокращается. Как в плоском, так и в трёхмерном случае. И вообще, когда декартовы компоненты скорости являются гармоническими функциями декартовых же координат.

Что из этого следует? Наверное то, что это "хорошие, годные" течения, работающие до какого-то предела, когда приходит турбулентность и ломает всю эту красоту.

[Ignatovich]

https://www.youtube.com/watch?v=YfmOrQyuZHg&list=PLeOlm2kq0HcskJ8WWrunWc_63k_jJmUOU&index=74
https://www.youtube.com/watch?v=3ntlBk4ji8c
..и есть еще две части.

[sergey zhukov]

Утундрий
А вот есть же, скажем, т.н. вторая вязкость $\zeta$, которая отвечает за диссипацию энергии в сжимаемой среде, т.е. при сжатии элемента жидкости. Почему же нет параметра вязкости, который отвечает за диссипацию энергии при деформации элемента жидкости? Точнее, как я понял, в потенциальном несжимаемом потоке диссипация энергии всегда равна нулю даже для вязкой жидкости, хотя деформация элемента там не нулевая. Но энергия рассеивается только при такой деформации элемента, когда $\operatorname{rot}(u)\ne 0$. Понятно, что при этом условии элементы "трутся друг о друга", поэтому энергия рассеивается. А разве она не рассеивается внутри самого элемента, когда он деформируется?

Поле скоростей осесимметричного или центральносимметричного радиальных потоков - это, наверное, один из немногих примеров, когда поле скоростей потенциально и при учете вязкости. Вероятно, да - это течение не может быть устойчивым.

-- 05.01.2023, 01:08 --

Ignatovich
Хорошие ролики. Довольно толковые. Автор пришел к тому же мнению, что и я: момент импульса уносится потоком в сток, который на практике нельзя сделать точечным. Если уменьшать диаметр стока, вращательный эффект стремится к нулю. В первом же приближении ответ на вопрос Фейнмана: вертушка вращаться не будет.

[wrest]

sergey zhukov в сообщении #1576240 писал(а):

Если уменьшать диаметр стока, вращательный эффект стремится к нулю.

А если увеличивать?

[sergey zhukov]

wrest
Если диаметр стока увеличивать, то это не обязательно, конечно, приведет к увеличению уносимого момента импульса: может, в такую дырку поток потечет строго радиально. Но потенциал у большого стока к отводу момента импульса больше. А если устремить его диаметр к нулю, то этот потенциал точно стремится к нулю.

[wrest]

sergey zhukov
Окей, значит получается так, что внутри вертушки образуется тормоз. А сила на входе в трубку все-таки образуется, т.к. вода в неё втекает все-таки не со всех сторон (при стремлении диаметра к нулю будет со всех). А если приделать фланец, то будет втекать из полусферы только.

[Утундрий]

sergey zhukov
Со второй вязкостью вопрос, по крайней мере для меня, тёмный.

[sergey zhukov]

wrest
Я еще немного подумал и предлагаю еще такое объяснение:


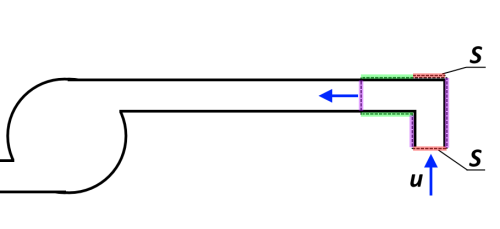
Для простоты рассмотрим вертушку с прямоугольными коленами трубок (это не принципиально). Нас интересует, действует ли на колено какая-либо сила (вертикальная составляющая этой силы в данном случае), когда в трубку всасывается среда? Сделаем простой расчет для идеальной жидкости.

Для этого окружим колено поверхностью так, как показано штриховой линией. Чтобы узнать, действует ли вертикальная сила на все, что попало внутрь поверхности, нужно вычислить поток вертикальной составляющей импульса через эту поверхность. Поток импульса через зеленые поверхности уравновешивается (давление одинаково, поверхности одинаковы). Поток импульса через фиолетовые поверхности имеет только горизонтальную составляющую. Фактически, нас интересует только поток импульса через красные поверхности $S$.

Поток импульса через нижнюю красную поверхность складывается из потока импульса с потоком вещества (он равен $(\rho u)uS=\rho u^2 S$) и потока импульса, связанного с давлением на нижнюю красную поверхность. В потоке идеальной жидкости выполняется уравнение Бернулли, т.е.:

$$\rho u^2+P=P_0$$

$P_0$ – давление атмосферы. Тогда поток импульса, связанного с давлением, через нижнюю красную поверхность есть $PS=SP_0-\rho u^2 S$. А поток импульса, связанный с давлением на верхнюю красную поверхность, есть $- SP_0$. Полный поток импульса равен:

$$\rho u^2 S+SP_0- \rho u^2 S-SP_0=0$$

.

Вывод – колено не испытывает вертикальной силы. Это верно для идеальной жидкости.

Более странно, что весь этот расчет остается совершенно таким же, если обратить поток. Так что в модели идеальной жидкости колено не испытывает вертикальной силы ни при каком направлении потока, хотя из практики мы точно знаем, что для прямого потока это явно не так. Так может, и в первом случае нет смысла доверять этой слишком идеализированной модели?

В этой упрощенной модели кое-что не так с давлением. В реальной вязкой жидкости давление падает вдоль линии тока по направлению движения жидкости (в сравнении с предсказанием уравнения Бернулли). Поэтому в прямом потоке давление максимально в центре вертушки, падает вдоль трубок к коленам, и на срезе сопла оно всегда выше на $\Delta P^+$, чем для идеальной жидкости из предыдущего расчета. Поэтому вертушка вращается соплом назад.

А при обратном потоке давление минимально в центре вертушки, возрастает вдоль трубок к коленам, и на срезе сопла всегда ниже на $\Delta P^-$, чем в идеальной жидкости. Поэтому вертушка вращается соплом вперед.

Если бы при одинаковой скорости прямого и обратного потоков было-бы $\Delta P^+=\Delta P^-$ , то вертушка вращалась бы в ту и другую сторону одинаково хорошо. Очевидно, что на практике $\Delta P^+>\Delta P^-$. Почему?

Дело в том, что $\Delta P^+$ может быть как угодно велико, нужно просто создавать внутри вертушки все бОльшее давление. А вот $\Delta P^-$ имеет вполне очевидный предел: оно не может понизить результат, который дает уравнение Бернулли, ниже нуля. Практически это означает, что давление на срезе сопла может как угодно сильно отклониться от формулы Бернулли в положительную сторону, но совсем немного – в отрицательную сторону.

Так, если уравнение Бернулли дает для некоторой скорости потока $u$ на срезе сопла давление, скажем $0,3P_0$, то для обратного потока обязательно $\Delta P^-<0,3P_0$. В то же время для прямого потока с той же скоростью уравнение Бернулли опять дает давление на срезе сопла $0,3P_0$, но при этом вполне может быть, что $\Delta P^+=10P_0$.

Это значит, что прямой поток значительно меньше похож на поток идеальной жидкости, чем обратный. Поэтому прямой поток создает сильный вращательный эффект, а обратный поток – слабый.

Поэтому в вязкой жидкости колено испытывает силу, которая заставляет вертушку вращаться. При этом при одной и той же скорости потока $u$ на срезе сопла прямой поток гораздо сильнее отклоняется от идеального (для которого сила нулевая), поэтому для него сила велика. А обратный отклоняется от идеального гораздо меньше, поэтому для него сила примерно нулевая.

Кстати, унос момента импульса в сток с потоком в этой модели не требуется. Для идеальной жидкости другого варианта объяснения обратного вращения нет, а для вязкой – есть.

[sergey zhukov]

И еще нужно отметить, что в практических опытах с вертушками, которые мы тут видим, нет гарантии, что скорость прямого потока равна скорости обратного. Тут последовательно ставят вертушку сначала в линию нагнетания, в затем - в линию всаса, но это не гарантирует, что расход воздуха будет равным в обоих случаях. Скорее всего, расход прямого потока получается выше.

Чтобы точно гарантироввть, что скорости потоков равны, нужно взять пылесос и установить одновременно две одинаковые вертушки на его входе и выходе. И сравнивать между собой скорости их вращения. Я думаю, они будут различаться меньше, чем когда одну вертушу подключают сначала на выход, а затем - на вход пылесоса.