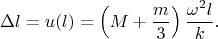Целую неделю "убил" на эту задачу. Вердикт таков: результаты уважаемых
lel0lel и
fred1996 будут совпадать в пределе малых деформаций (точнее когда интегральная относительная деформация мала). А это как раз то что нам нужно, поскольку в задаче требуется применение закона Гука в дифференциальной форме. в случае больших деформаций решение
lel0lel более корректно, поскольку учитывает измение поперечного сечения. Однако, при больших деформациях нужно учитывать и отклонения нелинейные от закона Гука (см. топик.
topic128791.html). Ниже приведу правильное "школьное" решение (уж простите за мой аглицкий).
Let us consider the homogeneous tourniquet of mass

and natural length

with stiffness
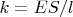
, where

is the Young's modulus,

is the cross-sectional area of the tourniquet. One of its end is fixed on a smooth table, and point mass

is attached to the other end. We assume that the tourniquet uniformly rotates in horizontal plane with an angular velocity of

. Let

be the horizontal coordinate of some cross-section before stretching. In this case, according to the Hooke's law, the absolute value of tension force

at the cross-section with coordinate

is equal to
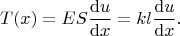
where
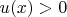
is the elongation of the tourniquet element of length

. Equation (1) (the linear theory) is valid for small deformations, where
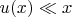
and
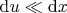
.
In the reference frame associated with the rotating tourniquet, the equilibrium equation of its infinitesimal element
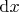
has the following form:
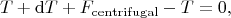
or
![$$
{\rm d}T(x) =-{\rm d}m \omega^2 \left[ x+u(x)\right] \approx -{\rm d}m \omega^2 x,
$$ $$
{\rm d}T(x) =-{\rm d}m \omega^2 \left[ x+u(x)\right] \approx -{\rm d}m \omega^2 x,
$$](https://dxdy-01.korotkov.co.uk/f/c/5/6/c5635070fb60971817331b1dd1e6f73982.png)
where
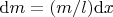
is the mass of the infinitesimal element
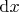
.
Using equations (1) and (2), we get:
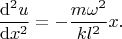
Hence
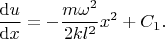
Since
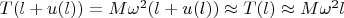
, then using equation (1), we obtain the integration constant:
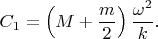
Therefore, in the case of
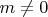
the deformation is inhomogeneous (
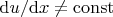
). Equations (1), (5), and (6) also tell us that the tension force is maximum at the tourniquet attachment point and decreases quadratically with increasing

-coordinate.
Considering again equations (5) and (6), we derive:
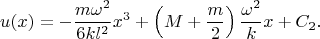
At


. Then
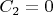
. Applying equation (7), we find the total elongation: