============================================================================================================================
n+0 n+1 n+2 n+3 n+4 n+5 n+6 n+7 n+8 n+9 n+10 n+11 n+12 n+13 n+14
45 722 841 12 49 50 507 32 961 18 605 28 867 1058 1369
p=Mod(438957010505237256671215545,440538835723387181869888800)
Decycle: 2 3 41 43 - repeats=10578
Check by index: 5 7 11 13 17 19 23 29 31 37
Numbers: 11
Primes up to 4093
============================================================================================================================

 не снизит конечно, зато остальные числа станут поменьше - и это и даст выигрыш скорости, ровно как и снижение
не снизит конечно, зато остальные числа станут поменьше - и это и даст выигрыш скорости, ровно как и снижение 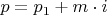 (за счёт снижения
(за счёт снижения  .
.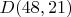 вида "3-0-13-5 (9)" и "4-0-12-5 (9)" такие, чтобы на месте с неизвестным простым стояло
вида "3-0-13-5 (9)" и "4-0-12-5 (9)" такие, чтобы на месте с неизвестным простым стояло 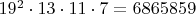 ?
?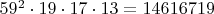 сделать, наверное ...
сделать, наверное ...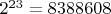 , но это уже изврат.
, но это уже изврат.
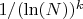 , где
, где  - длина цепочки.
- длина цепочки.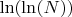 в какой-то степени, но для грубых оценок можно так считать.
в какой-то степени, но для грубых оценок можно так считать. порядков даёт такой же эффект, как увеличение количества паттернов на
порядков даёт такой же эффект, как увеличение количества паттернов на  до
до  . Оценку, наверное, надо будет сделать для наихудшего с
. Оценку, наверное, надо будет сделать для наихудшего с  .
. раздует LCM.
раздует LCM.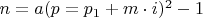
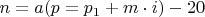
 ?
?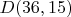 .
. ).
). 
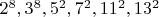
 менять на
менять на  не выгодно, а с другой стороны, менять
не выгодно, а с другой стороны, менять  на
на  тоже не выгодно.
тоже не выгодно. или
или  - нет.
- нет. .
.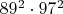 , остальные квадраты необязательных простых как-то расставляем.
, остальные квадраты необязательных простых как-то расставляем.
 , остальные пять необязательных простых в квадрате будем перебирать. Итого:
, остальные пять необязательных простых в квадрате будем перебирать. Итого: 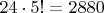 . Причем для них ускорители уже есть.
. Причем для них ускорители уже есть.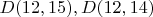 ?
? 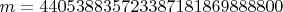
 , а так же того, что число кандидатов - это количество проверок после Длинного Ифа (нужно умножить на 2 - 2.5), всё оказалось очень похоже на правду.
, а так же того, что число кандидатов - это количество проверок после Длинного Ифа (нужно умножить на 2 - 2.5), всё оказалось очень похоже на правду.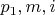 .
.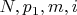 .
.