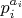Какую долю чисел вычеркивает решето Эратосфена?

[EUgeneUS]

Пусть задан конечный набор простых чисел и их степеней: $p_i^{a_i}$
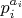
Простые числа - небольшие, до 100, иногда могут быть до 1000
Степени тоже не большие, до 10, чаще всего 1 или 2.

UPD: На всякий случай: $a_i \ge 1$, хотя выше написано, что $a_i$ - чаще всего 1 или 2.

Вычеркиваем все числа которые делятся на хотя бы одно $p_i^{a_i}$?

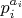
Вопрос: какая доля чисел вычеркнется, а какая останется.

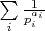
Наивная оценка в виде: вычеркнется $\sum\limits_{i}^{}\frac{1}{p_i^{a_i}}$, очевидна, неверна и сильно завышена.

А как в общем виде посчитать корректную оценку, что-то не соображу.

Если что, оценка нужна на больших числах - много больше любого $p_i^{a_i}$

[wrest]

Останутся невычеркнутыми только младшие степени простых, я правильно понял?

То есть например мы собрали конечный набор людей и вычеркиваем всех у кого одно и то же первое имя, кроме одного (младшего). Всех Иванов кроме младшего, всех Мухамедов кроме младшего и т.д. Ну тогда надо знать что-то дополнительно о наборе.

[EUgeneUS]

wrest в сообщении #1704281 писал(а):

Останутся невычеркнутыми только младшие степени простых, я правильно понял?

Набор простых в степенях, конечный.
Пусть такой $2^1, 3^2, 5^1$, тогда:
Вычеркнутся все четные, все, делящиеся на 9 и на 5.
Остальные останутся: $3, 7, 11, 13, 17, 21, 23, 29, 31, 33, 37, 39, 41, 43, 47, 49 .... $

Набор может содержать не обязательно самые младшие простые. Например, может быть таким:

$2^1, 3^1, 5^1, 7^1, 13^2$ ($11$ пропущено).

А, выше не написал, что $a_i \ge 1$, приношу извинения.

[wrest]

А, то есть вы вычеркиваете числа не внутри набора, а берёте натуральный ряд и вычеркиваете из него те числа, которые делятся на хотя бы одно из набора...

[EUgeneUS]

wrest
Да, именно так.
Причем интересует асимптотика, как-то так:
Пусть $D(N, 2N)$ - число вычеркнутых чисел из $[N, 2N)$.
Интересует $\lim\limits_{ N \to \infty}^{} \frac {D(N, 2N)}{N}$

[mihaild]

Считая, что все $p_i$ различны (иначе оставляем с минимальным $a_i$) - среди чисел, меньших $\prod_i p_i^{a_i}$, ровно $\prod_i \left(p_i^{a_i} - 1\right)$ не делящихся ни на одно из них, разве нет? Любой вектор остатков реализуется, причем ровно один раз. А дальше периодично.
Доля, соответственно, $\prod_i \left(1 - \frac{1}{p_i^{a_i}}\right)$.

[EUgeneUS]

mihaild
Спасибо!

Было понятно, что нужно делать поправки на все перекрестные произведения.
А оно очень компактно оказалось