Да, один из моих прогнозов сбылся в тот же день. Я дал его
до, а не после. Например, инфы о том, что огромный круг досчитался, у меня на 19 часов МСК ещё не было. Она появилась в 20 часов МСК(17 часов UTC).
если мы выбрасываем квадрат 37 с первого или последнего места в стандартном наборе паттернов, то все простые в конструкции
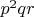
должны быть не меньше 37.
Собственно говоря, то же самое относится и к любому непроверяемому месту, с которого выбрасываем 37. Что за числа стоят на этих 8-ми местах? Они сравнимы с 25, 27, 29, 31, 33, 35, 37 и 39 по модулю 64.
То есть это должна быть четвёртая часть от всех ранее найденных
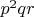
. Перепроверял. Пришлось честно считать три вложенных цикла, в том числе по

.
Код:
10^7 455 120
10^8 20774 5166
10^9 339702 84889
10^10 4121521 1030382
10^11 44375752 11094089
10^12 452718149 113180824
То есть пока 0.00011 от общего количества. Хорошо аппроксимировать пока не получилось, но прикинул, что доля таких чисел от общего количества к 34-й и тем более к 35-й степени упадёт до 0.00007.
Но считать надо не от общего количества, а от этих 8 чисел из 64-х. То есть вероятность увидеть
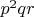
на любом из этих 8 мест в 8 раз больше:

Ну и накинув

на другие способы обнаружить здесь 12 делителей получаем

Вероятность обнаружить

на непроверяемом месте, если квадрат простого уже поставлен, была ранее неоднократно посчитана и равна примерно

для широкого диапазона.
Пока оценка очень грубая. Видимо, меньше чем

на другие способы. Ещё буду пересчитывать.