Starting relations:
bbb -> 1
aaaaaaab -> ba
aaaaaaaaaaaaaaaaaaa -> 1
Iteration: 1
Processing reations:
bbb -> 1
aaaaaaab -> ba
aaaaaaaaaaaaaaaaaaa -> 1
Expanding tree:
Depth: 18
Found: aaaaaaa -> babb
Proof: babb + b = ba = aaaaaaa + b
Iteration: 2
Processing reations:
bbb -> 1
aaaaaaa -> babb
aaaaaaab -> ba
Reduced
aaaaaaaaaaaaaaaaaaa -> 1
Reduced
Added: baabbaaaaa -> 1
Iteration: 3
Processing reations:
bbb -> 1
aaaaaaa -> babb
baabbaaaaa -> 1
Expanding tree:
Depth: 11
Found: abaabbaaaa -> 1
Proof: abaabbaaaa + a = a = 1 + a
Iteration: 4
Processing reations:
bbb -> 1
aaaaaaa -> babb
abaabbaaaa -> 1
baabbaaaaa -> 1
Removed
Found: baabba == abaabb
Proof: baabbaaaa + a = 1 = abaabbaaa + a
Iteration: 5
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
abaabbaaaa -> 1
Reduced
Added: aaaaabaabb -> 1
Iteration: 6
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaabb -> 1
Removed
Found: aaaaabaa -> b
Proof: aaaaabaab + b = 1 = bb + b
Iteration: 7
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaa -> b
Expanding tree:
Depth: 10
Found: abaaaaab -> bbaaaaa
Proof: abaaaaaba + a = abb = bbaaaaaa + a
Iteration: 8
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaa -> b
abaaaaab -> bbaaaaa
Expanding tree:
Depth: 9
Found: babaaaaa -> aaaaabb
Proof: babaaaaa + b = aaaaa = aaaaabb + b
Iteration: 9
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaa -> b
abaaaaab -> bbaaaaa
babaaaaa -> aaaaabb
Expanding tree:
Depth: 10
Found: baaaaaab == aababaaa
Proof: baaaaaaba + a = bab = aababaaaa + a
Iteration: 10
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaa -> b
abaaaaab -> bbaaaaa
baaaaaab == aababaaa
babaaaaa -> aaaaabb
Expanding tree:
Depth: 10
Found: bbaaaaaba == aaaabaabb
Proof: bbaaaaaba + a = 1 = aaaabaabb + a
Iteration: 11
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
aaaaabaa -> b
abaaaaab -> bbaaaaa
baaaaaab == aababaaa
babaaaaa -> aaaaabb
bbaaaaaba == aaaabaabb
Expanding tree:
Depth: 9
Found: bbaaaaa == aaabaab
Proof: aaabaabb + a = aaaabaabb = bbaaaaab + a
Iteration: 12
Processing reations:
bbb -> 1
baabba == abaabb
aaaaaaa -> babb
bbaaaaa == aaabaab
aaaaabaa -> b
abaaaaab -> bbaaaaa
Reduced
Added: baaa -> aab
Iteration: 13
Processing reations:
bbb -> 1
baaa -> aab
baabba == abaabb
aaaaaaa -> babb
bbaaaaa == aaabaab
Reduced
Added: aaabaab -> baabaa
Iteration: 14
Processing reations:
bbb -> 1
baaa -> aab
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
baaaaaab == aababaaa
Reduced
babaaaaa -> aaaaabb
Reduced
Added: baaabaa == aaaaabb
Iteration: 15
Processing reations:
bbb -> 1
baaa -> aab
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
baaabaa == aaaaabb
Reduced
Added: aaabb -> bbaa
Iteration: 16
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
bbaaaaaba == aaaabaabb
Reduced
Added: baabaaba == abaabaab
Iteration: 17
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
baabaaba == abaabaab
Expanding tree:
Depth: 8
Found: ababa -> bb
Proof: ababaa + a = bbaa = bba + a
Iteration: 18
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
baabaaba == abaabaab
Expanding tree:
Depth: 8
Found: aaabab -> babaa
Proof: aaabab + a = aabb = babaa + a
Iteration: 19
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
aaabab -> babaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
baabaaba == abaabaab
Expanding tree:
Depth: 8
Found: aaaaba -> bbabb
Proof: aaaaba + b = bba = bbabb + b
Iteration: 20
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
aaaaba -> bbabb
aaabab -> babaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
aaaaabaa -> b
Reduced
Added: abbabba -> b
Iteration: 21
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
aaaaba -> bbabb
aaabab -> babaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
baabaaba == abaabaab
Expanding tree:
Depth: 8
Found: baabab == aaaaaa
Proof: baabab + a = babb = aaaaaa + a
Iteration: 22
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
aaaaba -> bbabb
aaabab -> babaa
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
baabaaba == abaabaab
Expanding tree:
Depth: 8
Found: abaaba -> bab
Proof: abaaba + b = babb = bab + b
Iteration: 23
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
baabaaba == abaabaab
Reduced
Expanding tree:
Depth: 7
Found: bbaab -> aaa
Proof: bbaaba + b = aaaab = aaaa + b
Iteration: 24
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
bbaab -> aaa
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
Expanding tree:
Depth: 7
Found: babbaa == aababb
Proof: babbaa + b = aaba = aababb + b
Iteration: 25
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
bbaab -> aaa
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
babbaa == aababb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
Expanding tree:
Depth: 7
Found: bbaba == abbab
Proof: bbabab + a = b = abbabb + a
Iteration: 26
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
babbaa == aababb
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
Expanding tree:
Depth: 7
Found: babbab -> aba
Proof: babbab + a = abaa = aba + a
Iteration: 27
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
babbaa == aababb
babbab -> aba
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
Expanding tree:
Depth: 6
Found: babba == ababb
Proof: ababb + b = aba = babba + b
Iteration: 28
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
babba == ababb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
babbaa == aababb
Reduced
babbab -> aba
Reduced
aaaaaaa -> babb
aaabaab -> baabaa
abbabba -> b
Reduced
Added: ababab -> 1
Iteration: 29
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
babba == ababb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
ababab -> 1
Reduced
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
Expanding tree:
Depth: 8
Found: babaabb -> aaaba
Proof: babaabb + b = babaa = aaaba + b
Iteration: 30
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
babba == ababb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
babaabb -> aaaba
Expanding tree:
Depth: 8
Found: baabaabb -> aaabaa
Proof: baabaabb + a = aaaaab = aaabaa + a
Iteration: 31
Processing reations:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
babba == ababb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
babaabb -> aaaba
baabaabb -> aaabaa
Expanding tree:
Depth: 7
Graph has been finished.
Reduction set:
bbb -> 1
baaa -> aab
aaabb -> bbaa
ababa -> bb
babba == ababb
bbaab -> aaa
bbaba == abbab
aaaaba -> bbabb
aaabab -> babaa
abaaba -> bab
baabab == aaaaaa
baabba == abaabb
aaaaaaa -> babb
aaabaab -> baabaa
babaabb -> aaaba
baabaabb -> aaabaa

 для группы
для группы  , которая
, которая  и
и  .
. , где
, где  Здесь даже образующие одни и те же, то есть левые и правые наборы соотношений можно друг в друга преобразовать.
Здесь даже образующие одни и те же, то есть левые и правые наборы соотношений можно друг в друга преобразовать. Образующие общие (
Образующие общие (
 Элемент
Элемент  , которая получается добавлением соотношения:
, которая получается добавлением соотношения: 

 Образующие одни и те же. То есть одно из другого и наоборот должно получаться. Второе соотношение во втором наборе получается из второго и третьего соотношений первого набора очевидным образом, а с остальными надо повозиться.
Образующие одни и те же. То есть одно из другого и наоборот должно получаться. Второе соотношение во втором наборе получается из второго и третьего соотношений первого набора очевидным образом, а с остальными надо повозиться.
 Домножаем спереди на
Домножаем спереди на  Применяем первое соотношение справа в обратную сторону один раз, а слева — в прямую сторону
Применяем первое соотношение справа в обратную сторону один раз, а слева — в прямую сторону 

 Тут степени работают так: первое (обменное) соотношение при прогоне
Тут степени работают так: первое (обменное) соотношение при прогоне  Отщепляется одна степень
Отщепляется одна степень  Теперь подставляем в правую часть второе соотношение и делаем обратный прогон на два шага (отнимается 6 степеней, возвращается — 4-ре):
Теперь подставляем в правую часть второе соотношение и делаем обратный прогон на два шага (отнимается 6 степеней, возвращается — 4-ре):  Сокращаем, применяем полученное выше выражение для
Сокращаем, применяем полученное выше выражение для 
 В частности:
В частности: 
 Доказательство в обратную сторону. С последним соотношением всё понятно в обоих случаях это одно и то же, только справа оно переписано без отрицательных степеней. Остальные два:
Доказательство в обратную сторону. С последним соотношением всё понятно в обоих случаях это одно и то же, только справа оно переписано без отрицательных степеней. Остальные два: 





 имеет целую кучу компактных представлений. Некоторые из них:
имеет целую кучу компактных представлений. Некоторые из них: 
 которая в то же время является полупрямым произведением
которая в то же время является полупрямым произведением  может быть задана такими парами соотношений (малые степени расписаны в виде произведения для наглядности):
может быть задана такими парами соотношений (малые степени расписаны в виде произведения для наглядности): 



 В этих парах первое соотношение является обменным соотношением
В этих парах первое соотношение является обменным соотношением  , переписанным с учётом
, переписанным с учётом  , а второе (для первых двух пар) — с учётом
, а второе (для первых двух пар) — с учётом  При всём при этом, аналогичное соотношение из этой же серии
При всём при этом, аналогичное соотношение из этой же серии  задаёт группу 700-го порядка:
задаёт группу 700-го порядка:  Интересно, почему так получается?
Интересно, почему так получается? (которая по-другому не факторизуется) имеет следующие два кратких представления:
(которая по-другому не факторизуется) имеет следующие два кратких представления: 
 В первом образующие
В первом образующие 
 задают группу
задают группу  (с нулевым параметром получается просто
(с нулевым параметром получается просто  ), а соотношения
), а соотношения 
 задают некоторую разновидность
задают некоторую разновидность  , которая, как правило, имеет несколько других факторизаций. Надо бы это как-то строго доказать, за одно найти обменную степень полупрямого произведения во втором случае.
, которая, как правило, имеет несколько других факторизаций. Надо бы это как-то строго доказать, за одно найти обменную степень полупрямого произведения во втором случае. имеет задание
имеет задание  Сведение ко второй форме:
Сведение ко второй форме: 




 кроме краткого задания в образующих 3-8:
кроме краткого задания в образующих 3-8:  имеет ещё краткое задание в образующих 12-8:
имеет ещё краткое задание в образующих 12-8:  где первое соотношение не нужно (выводится из следующих двух; отправная точка — третья степень
где первое соотношение не нужно (выводится из следующих двух; отправная точка — третья степень  где
где  И даже такое задание тоже работает для этой группы в этих же образующих:
И даже такое задание тоже работает для этой группы в этих же образующих: 
 даёт интересную простую последовательность полупрямых произведений циклических групп, где коэффициенты довольно легко угадываются:
даёт интересную простую последовательность полупрямых произведений циклических групп, где коэффициенты довольно легко угадываются:
 из таблички, будут ли следующие группы конечными? Моя программка не нашла решения, но это означает лишь двойственность: либо группа слишком большая, либо бесконечная.
из таблички, будут ли следующие группы конечными? Моя программка не нашла решения, но это означает лишь двойственность: либо группа слишком большая, либо бесконечная. (если упростить
(если упростить 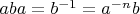 ), с его помощью можно избавиться от второго соотношения. Первое соотношение перепишем в виде
), с его помощью можно избавиться от второго соотношения. Первое соотношение перепишем в виде  и
и  . Поэтому
. Поэтому  и
и  , так что группа конечная (порядка не больше
, так что группа конечная (порядка не больше  ).
).