У меня есть функция:

, так вот мне нужно найти эту

, если известно, что
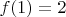
. Как я понял, нужно преобразовать функцию к виду

при

, уже туда подставлять эту единичку и смотреть, чему равна константа, но я вообще не понимаю, как это сделать не подбором. Более того, я искал в интернете подобные примеры, так там вообще просто говорят что-то типо: учитывая, что

можно сказать, что

, при этом имея функцию

. Вот у меня и возникли сомнения – может можно как-то проще подставить всё это дело, не преобразовывая функцию к

?