Мне интересно какой будет результат (с точки зрения КМ) и почему. И без формул ...
Кратко не получилось, и без формул не получилось, поэтому скрываю текст тегами оффтопа, чтобы он тут не маячил:
Без формул не обойтись: КМ требует вести анализ на основе главного в КМ понятия - комплексной амплитуды вероятности. Такого анализа нет в рассуждениях "1, 2, 3, 4", поэтому они не являются обоснованными с точки зрения КМ.
Опишу подробно один пример приемлемых рассуждений (притом всё-таки сильно упрощённый, без количественных деталей, он иллюстрирует ответ лишь качественного характера на вопрос "при каких условиях наблюдается интерференция?").
Пусть, наряду со щелями 1 и 2 и детектором электрона за щелями в точке

есть некие регистраторы 1 и 2, такие, что: регистратор 1 может обнаружить только прохождение электрона через щель 1, регистратор 2 может обнаружить только прохождение электрона через щель 2. Вероятность этих обнаружений может быть меньше единицы.
Тогда могут наблюдаться процессы (или, другими словами, "события", полностью описанные в терминах наблюдаемых актов срабатывания детектора и регистраторов) трёх различных типов:
а) сработал детектор

и сработал регистратор 1 (в таком случае обычно говорят: электрон пришёл в точку

через щель 1);
б) сработал детектор

и сработал регистратор 2 (в этом случае говорят: электрон пришёл в точку

через щель 2);
в) сработал детектор

а регистраторы 1 и 2 не сработали (тогда говорят: электрон пришёл в точку

или через щель 1, или через щель 2, - это так называемые неразличимые альтернативные реализации события

КМ-теория сопоставляет событиям (другими словами, процессам) комплексные числа, называемые амплитудами вероятности:
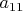
- амплитуда вероятности события а),

- амплитуда вероятности события б).
Здесь первым индексом обозначен номер щели, второй индекс - номер сработавшего регистратора. Аналогично обозначим и амплитуды вероятности для неразличимых альтернатив, но вместо номера регистратора напишем ноль, напоминающий нам о том, что ни один из двух регистраторов в случае в) не срабатывает:

- амплитуда вероятности придти электрону в

через щель 1 без обнаружения регистратором,

- амплитуда вероятности придти электрону в

через щель 2 без обнаружения регистратором.
В КМ-теории действует правило: по определению понятия "амплитуда вероятности", вероятность события равна квадрату модуля амплитуды вероятности. Причём, амплитуда вероятности события, которое описывается неразличимыми альтернативами, должна быть вычислена как сумма амплитуд вероятности неразличимых альтернатив. Таким образом:
Вероятность процесса а) есть

Вероятность процесса б) есть

Вероятность процесса в) есть:

где

означает число, комплексно сопряженное числу

Видим, что в случае в) выражение для вероятности содержит так называемый интерференционный член:

где

- разность фаз амплитуд вероятности

и

(Это равенство следует из формулы Эйлера

и из того, что всякое комплексное число

записывается в виде

сопряжённое число есть

Как такая теория учитывает возможность применять в опытах регистраторы со сколь угодно разными конструкциями?
Ответ: КМ учитывает это возможностью иметь разные значения амплитуд вероятности - они зависят от конкретики используемых в опыте устройств. (Вообще, амплитуды вероятности зависят от всей конфигурации опыта. В дальнейшем будет важно, что они зависят и от точки расположения детектора

Например, если регистраторы настолько сильно взаимодействуют с электроном, что ни в одном испытании они не "прозевают" электрон, т.е. если реализуются только события а) или б), вероятность же события в) равна нулю, то, значит,

Если при ином устройстве регистраторов их способность обнаруживать, через какую щель проходит электрон, ослаблена по сравнению с предыдущим примером, то, значит,

отличны от нуля, причём величины

стали меньше в такой постановке опыта - ведь теперь событие в) имеет вероятность отличную от нуля, и, значит, события а) или б), реализуются с меньшей вероятностью.
Наконец, если регистраторы совсем слабо связаны с электроном, то

при этом величины

стремятся к своим максимальным значениям. Предельные значения здесь достигаются при совершенно "слепых" регистраторах, как в опыте вообще без регистраторов.
Для ясности заодно напомню (занудно, но по другому у меня не выходит :), как выявляется в опыте обсуждаемая здесь в терминах КМ
интерференция. Опыт должен представлять собой много серий многих испытаний. Под одним испытанием подразумеваю одно прохождение электрона из источника через щели в детектор

или куда-то мимо этого детектора. Не экономная по времени, но лёгкая для понимания процедура вот какая:
В одной серии испытаний детектор электрона располагается всё время в одной и той же "точке"

(ну, или, в другом варианте опыта, мы сначала следим за попаданиями электрона только в заданную точку

на некоем большом детектирующем экране. Опыты показывают, что электрон всегда детектируется как частица, а не как какая-то волна; т.е. он не засвечивает большую площадь экрана, а именно ударяет в "точку"). Электронная пушка должна стационарно стрелять по щелям электронами с одной и той же энергией. Большинство электронов, попадают, разумеется, куда-то мимо данного детектора

даже если они попадают в щели; мы терпеливо накапливаем статистику попаданий в

В протокол с меткой

, строчка за строчкой, записываем (либо пусть автоматика записывает и подсчитывает) каждый факт попадания электрона в

и тип этого события: а), или б), или в). Всё это - в течение долгого времени

чтобы в протоколе накопилось много строчек.
В другой серии аналогичных испытаний детектор электрона сдвинут в другую точку. Записи накапливаем в новом протоколе, с новым значением

в течение такого же времени

И так далее. Процедура накопления статистики событий во всех сериях испытаний одна и та же, только положение детектора

разное.
Затем приступаем к оценке вероятностей. Для этого сортируем записи: подсчитываем в каждом протоколе (с конкретным значением

отдельно количество событий а), б) и в). Такие количества позволяют нам судить о частоте появления событий с заданным

Эти количества можно нормировать, разделив их на суммарное количество всех событий во всех протоколах, и принять результат за экспериментально найденную оценку вероятностей при заданном

Таким образом вероятности оцениваются на опыте как функции

,


Оказывается, что только функция

имеет характерный интерференционный вид - с чередой максимумов и минимумов. КМ-теория объясняет этот факт наличием интерференционного члена в выражении для

в нём есть косинус разности фаз

которая существенно зависит от

Теперь (т.е. уже с формулами :) легко пояснить общий недостаток рассуждений типа "1, 2, 3, 4" о возможности ослабления влияния регистратора на электрон будто бы такого, при котором и щель регистраторами определяется, и интерференция при этом не портится. Проблема - в "классичности" подобных рассуждений.
В КМ "слабость влияния" регистраторов означает просто малость соответствующих амплитуд вероятности и, следовательно,
редкость (малость вероятности) событий, в которых реализуется "слабое влияние". При этом такие события, т.е. процессы с регистрацией электрона у определённой щели, сколь бы редкими они ни стали из-за "совершенствования деликатности регистраторов", остаются принципиально
отличимыми от событий без регистрации - ведь на опыте тип событий прямо наблюдается и фиксируется в протоколах измерений, по которым затем подсчитывается статистика отдельно для каждого типа событий. Интерференционный характер имеет статистика событий, не сопровождавшихся определением пути, по которому шёл электрон (КМ объясняет это правилом сложения амплитуд вероятности
неразличимых альтернатив: оно порождает интерференционный член в формуле для вероятности).
Так что, в опыте даже с очень деликатными регистраторами интерференция будет видна в вероятности только тех событий, в которых не удавалось зарегистрировать электрон у конкретной щели. Деликатность регистраторов проявится в том, что таких событий будет большинство. А в вероятности событий со сработавшими регистраторами (при деликатных регистраторах таких событий будет просто мало) не окажется интерференции.
О сюжете со щелями и о роли понятия "амплитуда вероятности" советую также не полениться прочитать стр.10-12 в старенькой книжке Фейнмана "Теория фундаментальных процессов" (найти и скачать djvu-скан легко здесь:
eqworld. Изложение в ней крайне сжатое, конспективное, ни одного лишнего слова, поэтому читать надо не "по диагонали", очень вдумчиво. Желательно и дальше продвинуться - до стр. 14; и даже ещё далее, насколько удастся. Кстати, на стр. 164 там в очень сложный контекст вкраплено интересное сравнительно простое пояснение того, как в терминах амплитуд вероятности действует источник заданного внешнего поля (например, магнитного). Попробуйте заодно понять это место.)
На уже упомянутых стр. 10-12 рассмотрен случай, когда регистраторы электрона у щелей (работающие за счёт освещения электрона вспомогательным фотоном) никогда не "зевают" электрон, но могут иметь плохое разрешение, т.е. не могут достоверно различить, через какую из двух щелей электрон прошёл на детектирующий экран. Это описывается амплитудами вероятности

и

- они сопоставляются событиям, в которых регистраторы обнаруживают электрон не у "своей", а у "чужой" щели. В такой постановке опыта событий типа в) нет, а в статистике событий, подобных а) или б), проявляется интерференция амплитуд вероятности:

есть вероятность того, что сработал детектор

и сработал регистратор 1,

есть вероятность того, что сработал детектор

и сработал регистратор 2,
Если разрешающую способность регистраторов как-либо улучшить, то, значит, величины

и

уменьшатся. Значит, в этой постановке опыта интерференция подавляется с улучшением регистраторов, так как величины

и

входят в интерференционные члены множителями.
Короче говоря, в КМ всё диктуется "правилами композиции амплитуд вероятности": амплитуды вероятности неразличимых альтернатив суммируются и модуль суммы возводится в квадрат, а для различимых альтернатив амплитуды вероятности не суммируются. (Есть ещё и другие правила "композиции амплитуд", например: амплитуды вероятности событий, реализующихся последовательно, перемножаются. В нашем сюжете другие правила остались невостребованными).
Добавлю свои комментарии (их можно совсем не читать, ничего особо важного не потеряете :)
Почему в КМ-теории события описываются именно такими правилами? (Понятно, что потому, что именно такая КМ-теория хорошо согласуется с экспериментами, но вопрос в другом - почему экспериментальная картина в квантовой физике оказалась такой удивительной, что для её анализа требуется теория тоже удивительная (с точки зрения человека, привыкшего к физике классической)?)
Ответа на этот вопрос нет.
Могу предположить, что ответ появится, если когда-нибудь будут открыты явления и создана теория, объясняющие происхождение КМ-закономерностей. Сама КМ своё происхождение не объясняет (и не должна). Тем более, его не объясняют рассуждения, основанные на классической физике.
Хотя со времени создания КМ прошло уже почти 100 лет, и за это время сделано много попыток по-разному "интерпретировать" КМ, эти разные интерпретации не дали важных для практики новых результатов. КМ (и её релятивистское обобщение - модели КТП) остаётся теорией, количественно успешной в анализе реальных опытов и ценной для инженерной практики, именно как
статистическая теория событий. Количественно КМ особенно успешно работает в модельных системах с относительно небольшим числом частиц (а если и с большим, то в простых системах - в кристаллах, в частности. К макро-системам КМ не приспособлена, к макро-телам применяют, в зависимости от характера задачи, классическую механику или статистическую механику (включающую, в том числе, и квантовые аспекты)).
КМ и её понятие "амплитуда вероятности" не отвечает на вопросы об одном отдельно взятом событии; мол, "когда и где оно произойдёт?" (ну, кроме тривиальных ситуаций, типа "это событие не произойдёт, т.к. оно запрещено таким-то законом сохранения"). Но как статистическая теория, в которой понятие "амплитуда вероятности" относится к ансамблю событий и служит средством вычисления вероятностей, КМ полна - она предоставляет математический аппарат, достаточный для вычислений амплитуд вероятностей в разных задачах с
конкретно описанными моделями физических систем.
Думаю, есть отдалённая аналогия между, с одной стороны, обычной статистической механикой с её функцией распределения
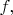
относящейся к ансамблю огромного числа частиц, и, с другой стороны, КМ с её распределением вероятности

относящимся к ансамблю событий в простых системах, в том числе в одночастичных задачах. Да, есть и важные различия: в статистической механике кинетическому уравнению подчинена сама
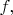
в отсутствие внешних возмущений она необратимо релаксирует к равновесной

В КМ уравнению динамики подчиняется не вероятность, а комплексная амплитуда вероятностей

(или, в других обозначениях,

динамика эта обратимая, описывается унитарным оператором эволюции. Кроме того,

тесно связана с внутренними и с пространственно-временными симметриями модели. Это позволяет в КМ для данной модели вычислять допустимые значения "физических величин", как спектры генераторов соответствующих групп симметрии; пример: генератором оператора эволюции является гамильтониан, его спектр - энергетический спектр системы. Однако всей этой спецификой КМ-теории не отменяется статистический смысл

найденный Борном ещё в 1926 г.
Резонно думать, что специфика КМ обусловлена пока ещё не раскрытой природой квантовой статистичности событий. Происхождение квантовой статистичности событий принципиально отлично от известных причин, по которым распределения вероятностей нужны в обычной статистической механике (там важны температура и тепловые флуктуации в многочастичных системах). На это указывает интерференционный характер вероятностей в КМ, и тот факт, что вероятности в КМ управляемы, очень чувствительны к параметрам системы; пример: дифракционная картина в опытах по рассеянию частиц на кристалле сильно изменяется просто при повороте кристалла относительно источника частиц или при изменении энергии частиц.
Поэтому, думаю, будущая теория, которая сумеет объяснить происхождение КМ с её удивительными "волновыми аспектами", должна будет вскрыть что-то очень глубинное, существенно новое в законах природы. И поэтому называться она должна будет уже не "КМ", а каким-то новым словом.
Такими же думами определяется и моё отношение к так называемым "интерпретациям КМ" - как к теориям с гипотезами, не проверенными явно в опытах и чуждыми КМ в её естественной статистической трактовке и в её сфере практических применений.
Так, с позиций упомянутой выше аналогии между

и функией распределения

гипотеза о коллапсе

в каждом испытании аналогична нелепой гипотезе (хорошо, что такую никто не предлагает! :) будто в статистической механике при экспериментальном изучении распределения частиц по объёму образца в каждом акте локального измерения плотности частиц функция распределения

чудесным образом коллапсирует в измеренное место, обнуляясь в остальных элементах объёма. Бессмысленна была бы и гипотеза, будто

описывает одну отдельно взятую реализацию статистического ансамбля. Ещё забавнее в статистической механике выглядела бы гипотеза о разветвлении миров; хорошо, что никто не говорит (или тут я ошибаюсь?), будто по ходу реализации быстрых тепловых флуктуаций в гигантском множестве всех имеющихся в природе тел постоянно родятся новые вселенные. По отношению к КМ аналогичное вольнодумство многие люди себе охотно позволяют (да ещё говорят, будто это не они, а КМ предсказывает подобные явления).
Конечно, я не против развития квантовой физики, не против поисков нового, не против исследований результатов применения мат. аппарата КМ в контексте необычных идей. Просто думаю, что, по-хорошему, следовало бы каждой новой гипотетической теории, хоть и порождённой изучением обычной КМ (статистической), но отличающейся от неё, давать своё совсем новое название. Чтобы в умах студентов не возникало путаницы с существующей полной КМ, не нуждающейся ни в каких дополнительных интерпретациях.