Но, повторюсь: если метрика может быть разрывной, то и статья китайцев, ссылку на которую выложил уважаемый physicsworks, ошибочна.
Я не понимаю, что именно разрывно при переходе через поверхность склейки. Если Вы говорите о разрывности компонент метрического тензора, то это является бессмысленным утверждением. По тривиальной причине: координаты по разные стороны от поверхности склейки
разные. Если мы смотрим на формулы

Здесь коэффициент

имеет разрыв на поверхности склейки

.
и думаем, что одинаково обозначенные координаты в этих двух строках — это одна и та же координата, то действительно у нас
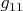
имеет разрыв при

. Однако, думая так, мы обманываем сами себя (и я не исключение). На самом деле надо было бы написать как-нибудь так:

И объяснить при этом, что на поверхности склейки выполняются равенства

,

,

,

.
Это, на самом деле, очень простой случай. В общем случае поверхность склейки в каждой из областей задаётся какими-то уравнениями

и

, а координаты одной стороны для точек этой поверхности выражаются через координаты другой стороны некоторыми функциями типа

,

,

,

. Как Вы там будете определять, непрерывны метрические коэффициенты или разрывны, я уж и не знаю. Уравнения связи действуют только на поверхности склейки, а их продолжения в окрестность этой поверхности сильно неоднозначны. Например если в формулах (27) в области

вместо координаты

ввести другую координату

(и для "упрощения обозначений" обозначить её снова буквой

), то получим

при всех

.
Нет, я уверен, что это условие сшивки не берётся аксиоматически, а каким-то образом обосновывается.
Следующий логичный шаг — вместо продолжения споров взять учебник и посмотреть, как обстоят дела на самом деле. Например, МТУ, том 2, § 21.13.