Разумеется нет, потому что от отображения

они никак не зависят.
Давайте рассмотрим пример. Прочитайте внимательно те пункты, которые я указал, и решите проверочную задачу:
Пусть у нас

- это пространство многочленов степени не более

(т.е.
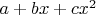
), в нем фиксирован базис
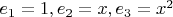
.

- это пространство многочленов степени не более

(т.е.
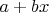
), в нем фиксирован базис
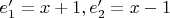
. Отображение

- это дифференцирование многочлена. Запишите матрицу этого отображения в паре базисов
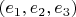
и
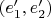
.
Желательно, чтобы Вы написали подробное решение, с промежуточными рассуждениями.
Если можно, я попытаюсь решить эту задачу позже, а пока у меня есть вопрос:
в
http://www.fipm.ru/matr3.shtml рассматривается отображение

с базисами соответственно

и

. Векторы

представляются в виде линейных комбинаций

...
Кажется, я начинаю понимать:

не может быть равно

, потому что

.
Это то, что и Вы сказали:
Меня интересует не матрица перехода (которая, кстати, определяется для двух базисов в одном пространстве, а не в разных), а матрица линейного отображения.

, поэтому рассматривается отображение

, то есть

.