Пусть у нас

- это пространство многочленов степени не более

(т.е.
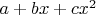
), в нем фиксирован базис
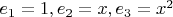
.

- это пространство многочленов степени не более

(т.е.
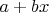
), в нем фиксирован базис
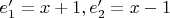
. Отображение

- это дифференцирование многочлена. Запишите матрицу этого отображения в паре базисов
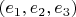
и
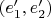
.
1.
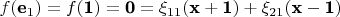
, где
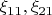
коэффициенты разложения вектора
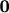
по базису
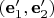
.
Используем приведенные выражения для
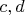
, заметив, что вектор
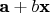
выражен здесь через базис
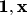
и координаты

.
Тогда
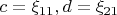
.
Выразим вектор
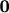
в базисе
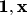
:
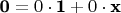
. Поскольку здесь
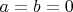
, получим
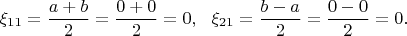
2.
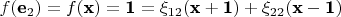
, где
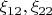
коэффициенты разложения вектора
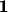
по базису
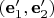
.
Теперь
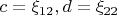
.
Выразим вектор
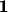
в базисе
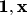
:
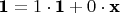
. Поскольку здесь
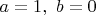
, получим
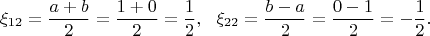
3.
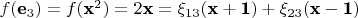
, где
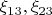
коэффициенты разложения вектора

по базису
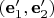
.
Теперь
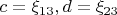
.
Выразим вектор

в базисе
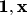
:
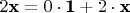
. Поскольку здесь
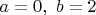
, получим
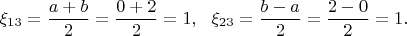
Таким образом,
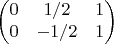
-- матрица отображения в паре базисов
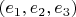
и
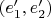
.