Всем добрый день!
Почитал я несколько учебников ТФКП, но никак не могу прояснить вопрос с конформностью и локальной конформностью ФКП.
Маркушевич говорит:
Отображение посредством непрерывной функции, сохраняющее углы между кривыми, проходящими через данную точку, называется конформным в этой точки .
При этом в дальнейшем обсуждается, что, коль скоро аргумент производной означает угол поворота, то всюду, где функция дифференцируема, она будет конформна, кроме, возможно, точек, где производная равна нулю (т.к. аргумент неопределен). Примера, когда производная нулю, но функция конформна в точке, не приводится (точнее, приводится, но не разбирается).
Шабат утверждает:
 -дифференцируемое в точке
-дифференцируемое в точке  отображение
отображение  называется конформным в точке
называется конформным в точке  , если
, если  - некритическая точка
- некритическая точка  и дифференциал
и дифференциал  в этой точке сводится к растяжению с поворотом
в этой точке сводится к растяжению с поворотом .
Хммм, Шабат в определении идет немножко по-другому. Но далее следует
Теорема 1
Пусть  - некритическая точка
- некритическая точка  -дифференцируемого отображения
-дифференцируемого отображения  . Для конформности
. Для конформности  в точке
в точке  необходима и достаточна его
необходима и достаточна его  -дифференцируемость в этой точке
-дифференцируемость в этой точке Обращу внимание, что про локальную конформность ничего нету. Ладно.
Откроем книгу попроще, задачник Краснова (в целом совсем неплохая книга для студентов-нематематиков). Сразу посмотрим критерий конформности (которая определяется как в Маркушевиче):
Для того чтобы отображение  было конформным в области
было конформным в области  , необходимо и достаточно, чтобы в этой области функция
, необходимо и достаточно, чтобы в этой области функция  была однолистной и аналитической, причем
была однолистной и аналитической, причем  для всех
для всех  .
. Тут уже почему-то говорится об однолистности, и далее следует то, что мне вообще непонятно. Рассматривается функция

в области

,

. Делается вывод о том, что она неоднолистна в этой области, а значит и неконформна. Но несколько строчек ниже уже рассматривается

всюду на

, которая, на мой взгляд, тоже неоднолистна, но при этом утверждается ее конформность (кроме одной точки
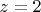
, хотя ее неконформность в этой точке никак не доказывается).
Дорогие друзья, помогите мне, пожалуйста, понять, что такое конформность, что такое локальная конформность, где и когда нужна однолистность и как исследовать конформность в случае, когда

. Спасибо большое!