Someone писал(а):
Ваших аксиом 1 и 2 в теории множеств нет. Вместо первой используется аксиома бесконечности, а вторая аксиома не нужна вообще, потому что выбор из конечного семейства (дизъюнктных) непустых множеств осуществляется без всяких аксиом: если

, то по определению

, вот его и возьмём. Для конечного семейства множеств это рассуждение нужно повторить конечное число раз. Для бесконечного же семейства множеств нужна специальная аксиома, потому что бесконечные рассуждения доказательствами не считаются, поскольку их невозможно закончить.
Существует более чем достаточно аксиоматик теории множеств и пока никто не доказал, какая из них самая главная. В том числе неоднократно осуществлялись попытки избавиться от бесконечностей, прийти к конструктивизму, интуицивизму и т.д. и т.п.
Сама по себе задача находится на грани фола, потому и возникают проблемы.
Someone писал(а):
Обсуждаемое построение как раз является примером такого бесконечного построения и, строго говоря, его нужно формализовать, чтобы никаких бесконечных рассуждений при этом не возникало.
Фактически здесь по индукции строится последовательность множеств

следующим образом:
1)

;
2)

при
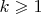
.
Задача же состоит в вычислении множества

.
Формализуя рассуждение Вы как раз и пользуетесь предельным переходом, что видно уже из Вашей формальной записи, да ещё и на индукцию ссылаетесь...
Сами по себе понятия связанные с понятием бесконечности неоднозначны в математике. Например, в евклидовой геометрии говорить о бесконечно удаленной точке не принято, её как бы и нет, а в проективной геометрии она вводится и система окресностей для бесконечно удаленной точки имеет тот же вид, что для любой другой "бесконечно неудаленной". В этом случае бесконечность косвенным образом (через бесконечную точку) актуализируется. Тоже самое происходит при другом выборе аксиом - понятие бесконечности принимает другое содержание. Это считается нормальным, это в духе "основного русла", хотя по сути "бесконечность" в каждом из случаев имеет различный смысл.