Давайте уточним: множество

в
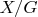
открыто, если

открыто в

Это. И ещё "если" заменить на "тогда и только тогда".
о исходя из Вашего предыдущего сообщения вытекает, что естественное отображение

должно быть непрерывным и открытым одновременно.
Непрерывным да, открытым необязательно. (Как вы и показали примером с

)
либо совокупности счётного числа открытых интервалов, каждый из которых содержит внутри себя не менее одного натурального числа.
+ каждое натуральное число содержится хотя бы в одном открытом интервале, наверняка вы это и хотели написать. В остальном вы правы. (Ну это не все, но такие формируют базу).
И если да, то что это нам даёт в плане вопроса об отсутствии первой аксиомы счётности в факторе ? Буду благодарен за Ваше мнение !
От противного, предположите что у класса

есть счётная база

взяв прообразы обратно в

получите семейство интервалов

где

окрестность точки, собственно,

. Используйте диагональный аргумент чтобы построить открытое множество содержащее

но при этом не содержащееся в

для любого

, это вам даст окрестность в
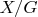
не содержащуюся ни в одном элементе базы

, что приведёт к противоречию.