Утверждение вообще весьма общее. Разрывность, мёбиусовость и даже хаусдорфовость ни при чём.
Предложение. Пусть  --- топологическое пространство,
--- топологическое пространство,  --- группа гомеоморфизмов
--- группа гомеоморфизмов  . Допустим, что
. Допустим, что  имеет базу открытых множеств мощности
имеет базу открытых множеств мощности  . Тогда
. Тогда 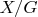 тоже имеет базу мощности
тоже имеет базу мощности  . Доказательство.
. Доказательство. Как множество,
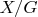
--- это множество всех орбит

. Топология на
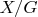
, по определению, задается тем, что

открыто тогда и только тогда, когда объединение орбит, входящих в

, открыто в

.Можно еще сказать так: открытые множества в
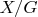
--- это

-инвариантные открытые множества в

.
Для любого подмножества

обозначаем

.
Если

открыто, то все

открыты, значит,

открыто. Поэтому естественное отображение

открыто.
Пусть

--- база открытых множеств для

. Мы утверждаем, что

--- база для
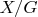
. Отсюда будет следовать нужное утверждение, так как мощность последнего множества не больше, чем мощность

.
Нам достаточно доказать, что для любого

-инвариантного открытого множества

, и любого

такого, что

, существует

такое, что

. Пусть

--- некоторое множество из базы такое, что

Поскольку

, то

. Поскольку

---

-инвариантно и

, то

. Значит,

обладает нужными свойствами.

Литература:
Бурбаки, Общая топология (русское изд. 1968-69 г.), гл.3.
Топологические группы (элементарная теория)