Помогите разобраться в решении интеграла

[Svinks]

Здравствуйте, мне нужно произвести расчёт выбросов радиоактивных веществ в атмосферу. Беда заключается в том, что у нас в КБ никто не умеет работать с интегралами, с таким случаем я еще никогда не сталкивался.

Имеется интеграл:

$$\Phi(x) = \exp \left[ -\sqrt{\frac{2}{\pi}} \frac{V_g}{u} \int\limits_{0}^{x} \frac{1}{\sigma_z(x)} \exp \left( -\frac{(h_s+H(x))^2}{2\sigma_z(x)^2} \right) dx \right]$$

Взято уравнение отсюда http://docs.cntd.ru/document/1200072232 формула (П4.42)
Сигма считается по формуле (П4.22).

Как мне раскрыть это уравнение? Я могу, например, заранее посчитать сигму, и вставить его в интеграл? Или я должен вписать все функции в этот интеграл, затем раскрывать его?

[wrest]

Svinks
А что вам нужно в качестве результата "раскрытия уравнения"?

Сигма, судя по описанию П4.22, может оказаться и константой (не зависеть от расстояния), тогда её надо просто подставить как константу.
$H$ кстати тоже константа, от расстояния не зависит, так ведь?

Если, в итоге, подыинтегральное выражение от переменной интегрирования (расстояния) не зависит - вам повезло (получается интеграл от константы). Если зависит, то тогда надо будет "вписать функции в интеграл".

[Svinks]

А как мне понять, константы те переменные или нет? Я их по методике подсчитал для разных расстояний уже, но мне дальше нужно посчитать по этому уравнению.

Я хочу убрать интеграл, чтобы получить формулу без него.

-- 15.01.2019, 10:59 --

И не понятно, если там все константы, зачем авторы методики записали это в интегральном виде?

[EUgeneUS]

Svinks в сообщении #1368803 писал(а):

А как мне понять, константы те переменные или нет? Я их по методике подсчитал для разных расстояний уже, но мне дальше нужно посчитать по этому уравнению.

Если Вы посчитали, для разных расстояний, то либо
а) они получились одинаковыми (с точностью расчетов), тогда константы.
б) они получились разными, тогда не константы.

wrest в сообщении #1368802 писал(а):

Сигма, судя по описанию П4.22, может оказаться и константой (не зависеть от расстояния), тогда её надо просто подставить как константу.

Может оказаться константой, а может и не константой, а может на некотором участке константой, а на другом - нет. Судя по П4.22.

ИМХО, численными методами надо считать.
ЗЫ, Скорее всего есть какая-нибудь поделка-САПР от Росатого (за сотни нефти), где это все и считается.

[wrest]

Svinks в сообщении #1368803 писал(а):

И не понятно, если там все константы, зачем авторы методики записали это в интегральном виде?

Потому что могут быть и не константы: смотрите что написано про сигму в П4.22

Svinks в сообщении #1368803 писал(а):

Я хочу убрать интеграл, чтобы получить формулу без него.

Ну если бы это можно было бы, то в книжке сразу эта формула и была бы Кстати посмотрите на формулу П4.43 -- в ней учтено, что на части промежутка интегрирования подынтегральное выражение может быть константой, видите там пределы интегрирования другие?

Реальная жизнь сложна, в ней интегралы не очень табличные могут быть, так что вам поможет численное интегрирование. Ещё может помочь внимательное смотрение на подыинтегральную функцию, из чего она состоит. Как эта функция вообще меняется от начала к концу промежутка интегрирования? Эта сигма -- довольно развесистое выражение, там несколько еще параметров участвуют.

Можете нарисовать график подынтегральной функции в пределах интегрирования?

-- 15.01.2019, 10:31 --

EUgeneUS в сообщении #1368807 писал(а):

Может оказаться константой, а может и не константой, а может на некотором участке константой, а на другом - нет. Судя по П4.22.

Да, там до какого-то расстояния $x_{max}$ сигма меняется, а потом нет, это типа учтено в П4.43

Svinks
Ещё хочу заметить, мне кажется, что знаменатель показателя последней экспоненты записанный как $-\dfrac{H^2}{2\sigma_z(x)^2}$ следует читать как $-\dfrac{H^2}{2(\sigma_z(x))^2}$ (а не как $-\dfrac{H^2}{2\sigma_z(x^2)}$) -- обратите внимание на это.

[Svinks]

По поводу квадрата вы правы. Как провести численное интегрирование? Я абсолютно тут плаваю, нужен алгоритм действий :(

Маткад может этот интеграл найти?

[ET]

(Оффтоп)

Извините за оффтоп, но у нас за такое вот заказчику руки отрывают

Svinks в сообщении #1368798 писал(а):

$\int\limits_{0}^{x} .... dx$

Ведь теперь интеграл можно понимать в данном случае 8ю разными способами. Более того - я подозреваю, что в случае ТС тот $x$, который $H(x)$ в данном случае - это именно константа, то есть внешний $x$
Еще раз сорри за оффтоп, хочу спросить знающих, это нормально?

[wrest]

Svinks в сообщении #1368815 писал(а):

Как провести численное интегрирование?

Ну я не знаю какие средства у вас есть для этого. Есть программы типа MathCAD ("MathSoft Inc.", http://www.mathsoft.com), MatLAB ("MathWorks", http://www.mathworks.com), Maple V (“Waterloo Maple Software”, http://www.maplesoft.com), Mathematica (“Wolfram Research Inc.”, http://www.wolfram.com) и т.п.
Вот например как это можно сделать в экселе методом трапеций: https://soltau.ru/index.php/themes/komp ... j-integral

Но начните хотя бы с графика подыинтегральной функции - его вы можете построить?

-- 15.01.2019, 11:33 --

ET в сообщении #1368817 писал(а):

Еще раз сорри за оффтоп, хочу спросить знающих, это нормально?

Я дилетант, но мне это тоже кажется не вполне нормально. Ясно что одна и таже буква в пределах интегрирования и как переменная в подыинтегральной функции это наверное неправильно, они должны быть разные, но понять как-то можно.

[StaticZero]

Svinks, для начала надо бы разгильдяйство убрать и понять, наконец, какая переменная интегрирования и кто там параметр. Моя гипотеза такая:

$$\Phi(x) = \exp \left[ -\sqrt{\frac{2}{\pi}} \frac{V_g}{u} \int\limits_{0}^{x} \frac{1}{\sigma_z(x')} \exp \left( -\frac{(h_s+H(x'))^2}{2\sigma_z^2(x')} \right) dx' \right]$$

(Забавно, что это самое разгильдяйство кочует из источника в источник и никто не задумывается; видимо, всём всё понятно.)

Скорее всего, здесь необходимы квадратурные формулы, а, значит, и таблица значений $H(x')$, $\sigma_z(x')$ на промежутке $[0, x]$. Ваш интеграл тогда будет превращён в серию интегралов вида $I(x) = \int \limits_0^x = \int \limits_{x_0 = 0}^{x_1} + \int \limits_{x_1}^{x_2} + \ldots + \int \limits_{x_{n-1}}^{x_n = x} = I_1 + I_2 + \ldots + I_n$. Каждый интервал $[x_{k-1}, x_k]$ длины $h_k = x_k - x_{k-1}$ заменой переменных $t_k = 2\cdot \frac{x - x_{k-1}}{h_k} - 1$ можно обратить в интервал $[-1, 1]$. В этом случае на соответствующем интервале

$$ f(x) = f\left(\frac{(t_k + 1) h_k}{2} + x_{k-1}\right) \equiv F_k(t_k) $$

и интеграл превращается в

$$ I_k = \int \limits_{x_{k-1}}^{x_k} f(x) \ \mathrm dx = \frac{h_k}{2} \int \limits_{-1}^1 F_k (t_k) \ \mathrm dt_k. $$

На интервале $[-1, 1]$ можно выбрать узлы $g_1, g_2, \ldots, g_p$ и применить квадратурную формулу вида

$$ \int \limits_{-1}^{1} F_k \left(t_k\right) \ \mathrm dt_k \approx \sum \limits_{s=1}^p w_s F_k(g_s), $$

где $w_s$ --- веса узлов. Каковы именно эти узлы и веса --- зависит от квадратурной формулы. Например, для формулы типа Гаусса первого порядка нужно задать $g_1 = 0$, $w_1 = 2$; для второго порядка - $g_1 = -1/\sqrt 3$, $g_2 = 1/\sqrt 3$, $w_1 = w_2 = 1$ и т. д.

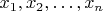
Это процедура, которую можно выполнить и самостоятельно. Построение, конечно, зависит от того, как хорошо затабулирована подынтегральная функция. Вы можете таким способом получить значения интеграла $I(x)$. Они будут задаваться в форме таблицы. При этом наиболее выгодно построить вычисления так: если вам нужен $I(x)$ в точках $x_1, x_2, \ldots, x_n$, то тогда точки деления отрезка в процедуре удобно выбрать именно этими; вы можете тогда построить следующую точку $I(x_{n+1})$, просто прибавляя к $I(x_n)$ результат интегрирования по малому промежутку $[x_{n+1}, x_n]$, который легко берётся (с помощью замены и квадратурной формулы). Такая процедура нахождения значений в таблице масштабируема и регулярна. Значения $\Phi(x_n)$ тогда тупо получаются взятием нужной экспоненты от $I(x_n)$.

[wrest]

StaticZero в сообщении #1368832 писал(а):

для начала надо бы разгильдяйство убрать и понять, наконец, какая переменная интегрирования и кто там параметр. Моя гипотеза такая:

$$\Phi(x) = \exp \left[ -\sqrt{\frac{2}{\pi}} \frac{V_g}{u} \int\limits_{0}^{x} \frac{1}{\sigma_z(x')} \exp \left( -\frac{(h_s+H(x'))^2}{2\sigma_z^2(x')} \right) dx' \right]$$

(Забавно, что это самое разгильдяйство кочует из источника в источник и никто не задумывается; видимо, всём всё понятно.)

В источнике, на который ссылается ТС, показатель подынтегральной экспоненты записан так:
$ -\dfrac{H^2}{2\sigma_z(x)^2}$ и поясняется что $H$ - эффективная высота выброса, м; То есть $H$ -- константа, а не функция расстояния. А вот $\sigma_z(x)$ - это функция, зависимость вертикальной дисперсии распределения примеси в струе выброса от расстояния. Которая меняется при изменении $x$ от нуля до какого-то $x_{max}$, при котором $\sigma_z(x)$ достигает максимального значения $\sigma_z(x_{max})=\sigma_z^{max}$ после чего остается постоянной, равной $\sigma_z^{max}$

[StaticZero]

wrest в сообщении #1368833 писал(а):

То есть $H$ -- константа, а не функция расстояния

Я в этом случае следую ТС, он мог изменить формулу, добавив зависимость, чтобы учесть что-то ещё (а мог просто лишний аргумент засунуть там, где его нет).

[Svinks]

Я раньше не строил данный график. И честно говорю, последний раз имел дело с интегралами 6 лет назад
пытаюсь вникнуть. По поводу разгельдяйства, приведу позже скриншот оригинальной формулы. Тот что по сылке по старому документу.
За помощь большая благодарность, буду сидеть осмысливать. Я пока плохо понимаю то, что вы сделали.

[wrest]

Svinks в сообщении #1368835 писал(а):

Я раньше не строил данный график.

Напрасно, вдруг там прямая линия или на неё очень похоже?

[StaticZero]

Н. Н. Калиткин. Численные методы, глава IV.

Ещё можно методом посмотрения попытаться определить, есть ли хорошая глобальная на $[0, x]$ аппроксимация для подынтегральной функции. Если она есть, то можно взять аппроксимирующую функцию простого вида и её проинтегрировать уже аналитически, но тогда с оценкой погрешности повозиться необходимо, ибо без неё оно всё выглядит неубедительно.

[Svinks]

https://cdn1.savepice.ru/uploads/2019/1 ... 6-full.png

https://cdn1.savepice.ru/uploads/2019/1 ... 3-full.png

https://cdn1.savepice.ru/uploads/2019/1 ... 4-full.png

https://cdn1.savepice.ru/uploads/2019/1 ... 6-full.png

(Оффтоп)

не спорю, что у меня объемно-плоские извилины головного мозга. Повторюсь, задача для нашего КБ не стандартная. С интегралами имеют дела раз в 10 лет. И то посылают на интегральный убой новичков, подобных мне :)

поясните пожалуйста в чём разгильдяйство, не доходит