Уединенные проводящие поверхности

[AnatolyBa]

Alex-Yu в сообщении #1362967 писал(а):

Если эти поверхности окажутся сферами --- то все ОК

Нет, не совсем сферами. У Смайта есть решение для двух сфер - метод отражения, бесконечное количество фиктивных зарядов. Решение в виде ряда. Но в данном случае нет смысла влезать в эти дебри.

shaxel в сообщении #1362972 писал(а):

потенциал на уровне 1МВ и более легко получить даже с этой не идеальной конструкцией

Чего-то в этом роде я и боялся.
Знаете, должен признаться, я иногда нарушал технику безопасности. Но я всегда знал, что я нарушаю и почему. Судя по вашим словам - я очень не рекоммендую вам играть с высоким напряжением

[LMA]

Согласно Смайту емкость системы

$$C=8\pi\varepsilon a \sh(\beta)\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{\sh(n\beta)},$$

где $\beta=\frac{1}{2}\operatorname{arch}\left(\frac{c^2}{2a^2}-1\right),$ $a$ - радиус одного шара, $c$ - расстояние между центрами шаров.
На графике ниже по оси абсцисс - расстояние между центрами шаров, деленное на радиус, по оси ординат - емкость системы, деленная на емкость одного шара.

Ответ на первый вопрос shaxel: емкость второй системы больше примерно в 1.07 раза (конечно без учета свисающего проводника).

[shaxel]

Спасибо! Для меня это неоценимая помощь. Отблагодарил бы от души, если б знал как...
7% - маловато будет, черт возьми, очень мало. Слишком тонкая настройка получится.
На самом деле я очень хорошо себе представляю что делаю, если это действительно заработает так как я на то рассчитываю, это будет просто пример реального чуда!

У меня был еще один первоначальный вариант, и я даже купил шары и начал все это дело пилить и собирать, но потом обнаружил проблему. Система задумывалась, как 2 шара, один диаметром 12 см, второй диаметром 10 см. Больший шар спиливается так, чтоб отверстие в нем получилось чуть более 10 см. Шары садятся на общую проводящую ось t как показано на рисунке и больше нигде не контактируют между собой.

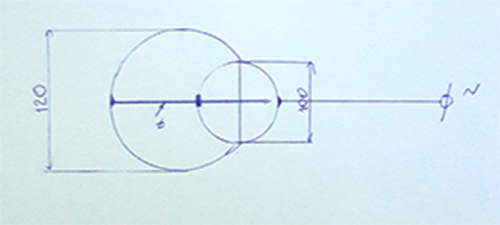
Но потом подумал, что заряд, попадая на меньшую сферу, распределится по всей ее поверхности, потом по оси попадет на большую сферу и пойдет как-бы в обратном направлении, доходя до нижних краев большей сферы, начнет вытеснять заряд с "погруженной" поверхности меньшей сферы, то есть эта система даст маленькую обратную волну. В конечном итоге получится какофония.
От этого недостатка можно было бы избавиться, соединив проводником кромку по обрезу большей сферы, скажем, с экватором меньшей, и сделать ось диэлектрической, но проблема в том, что этот проводник должен иметь свойство растягиваться и быть максимально гладким. Иначе я не смогу вкручивать и выкручивать меньший шар.
Блин, были бы бабки, заказал бы на заводе 2 вкручивающиеся друг в друга полусферы, а так приходятся мутить из ... конфетку.

-- 22.12.2018, 11:11 --

LMA, а Вы не ошиблись сказав 1.07 раза?
Например, емкость одного шара 3 пФ.
Вариант 1: они прислонены друг к другу, по графику получается емкость такой системы - 4,11 пФ примерно.
Вариант 2: расстояние между их краями равно двум радиусам (между центрами - 4 радиуса), емкость системы - 4,8 пФ
Разница 16,7 % это уже лучше!
Только что посчитал используя график, получились такие цифры.
А, нашел ошибку свою: у меня на рисунке первый вариант - между шарами уже есть расстояние.
Вывод: такая система может дать до 20% настройки емкости примерно. В принципе, этого должно быть достаточно. С учетом того, что такую систему сделать достаточно просто используя недорогие комплектующие, можно сделать 2-3 пары сменных систем. Скорее всего, я так и поступлю.

[AnatolyBa]

LMA
Интересно сравнить мои прикидки с вашей формулой.
Я дал две цифры - разница между случаем когда шары рядом и когда расстояние 2 диаметра (4 радиуса) - я дал 50%, у вас где-то 20.
Тут я собой недоволен. Вторая цифра - емкость двух шаров по сравнению с емкостью одного шара. Я дал 35%, у вас где-то 39. Тут я доволен.
А теперь, почему я не хотел напрямую пользоваться формулой Смайта. Дело в соединяющем шары проводке. Конечно, его емкостью можно пренебречь, но он искажает поле и чем дальше шары, тем искажение сильнее. Это сказывается на взаимной емкости и формула Смайта становится неточной.
P.S.
Посмотрел свои прикидки. Оказывается я вычислил 50% из предположения очень далеко удаленных шаров. Если действительно взять 2 диаметра, получается 28%. Ну что-ж, ничего

[DimaM]

Alex-Yu в сообщении #1362967 писал(а):

Может аналогичный трюк сработает и для шаров. Нужно просто посчитать потенциал двух точечных зарядов и попытаться найти эквипотенциальные поверхности. Если эти поверхности окажутся сферами --- то все ОК, дальше очевидно. Тогда можно решить без приближения большого расстояния. Если этот трюк не срабатывает, то ничего не поделать: только численно решать граничную задачу. Но интуитивно кажется, что должно сработать.

Для шаров известно, что не сработает.

[nds]

shaxel в сообщении #1362972 писал(а):

Делаю то что изображено на аватаре, только вместо каждого из двух шаров на концах будет применяться рассматриваемая система, потенциал на уровне 1МВ и более легко получить

А что за конструкция такая, если не секрет? По аватарке не очень то понятно)

Чтобы понизить утечки на коронный разряд можно отполировать шары.

[shaxel]

Ну я аналогию очень краткую указывал выше что это такое. Зачем это надо расписывать не хочу чтоб просто на смех не подняли, да и что бы Вы не думали, многие моменты просто не хочу раскрывать...
Шар будет максимально отполированным, кроме того, он будет иметь меридианные разрезы для минимизации нагрева из-за индуцируемых на его поверхности токов. Если совсем точно, то это будет пластмассовый елочный шар, оклеенный тонкими плотнячком расположенными полосками алюминия по меридианам. Эта конструкция значительно снизит вес. Есть цельные стальные сферы, но они тяжелые - усложнится монтаж. Достать цельный алюминиевый шар сложно и дорого.

[wrest]

shaxel
А шары из эстетических соображений? Просто вот взять что-то телескопическое, типа телескопической антенны и раздвигать-задвигать. Емкость будет меняться по совершенно предсказуемой формуле для цилиндра (нетолстого проводника).

[shaxel]

Нужны поверхности максимально приближенные к сфере, то есть радиус кривизны нужен максимальный, почти только от этого будет зависеть получу я 10 кВ или 1 МВ на шаре... Есть еще идея, что системы из 2-х шаров по краям можно заменить только одним шаров на телескопической стойке. Если рассматривать саму установку, что видно на аватаре, то она уже сама по себе будет иметь 2 шара. Просто вопрос в том, что между ними будет переменное магнитное поле слабой напряженности и электрическое поле очень большой напряженности плюс проводящие и диэлектрические конструкции. Посчитать все это для меня не реально. Когда-нибудь попробую это проверить экспериментально, или закажу расчет у крутого математика.

[LMA]

AnatolyBa
Да, точно, проводок исказит. Это я проглядел.

shaxel
Вот код для FreeFem++:

1. real a = 1; 
2. real c = 6*a; 
3. real rs = (c/2 + a)*4; 
4. border b1(t = 0, rs) {x = t; y = 0;}; 
5. border b2(t = 0, pi/2) {x = rs*cos(t); y = rs*sin(t);}; 
6. border b3(t = rs, c/2 + a) {x = 0; y = t;}; 
7. border b4(t = pi/2, -pi/2) {x = a*cos(t); y = c/2 + a*sin(t);}; 
8. border b5(t = c/2 - a, 0) {x = 0; y = t;}; 
9.  
10. mesh Th = buildmesh(b1(10) + b2(10) + b3(10) + b4(10) + b5(5)); 
11. fespace Vh(Th, P2); 
12. Vh u, v; 
13.  
14. problem problem1(u, v) = int2d(Th) ((dx(u)*dx(v) + dy(u)*dy(v))*x) 
15.     + on(b4, u=1) + on(b2, u=0); 
16. for (int i = 0; i < 3; i++) 
17. { 
18.     problem1; 
19.     Th = adaptmesh(Th, u); 
20. }; 
21. problem1; 
22. plot(u, fill = true, value = true); 
23.  
24. real capacitance = int2d(Th) ((dx(u)*dx(u) + dy(u)*dy(u))*2*pi*x); 
25. capacitance = 1/(1/(2*capacitance) + 1/(4*pi*rs)); 
26. cout << "capacitance/(4*pi*a) = " << capacitance/(4*pi*a) << endl; 

Результат:

Цитата:

capacitance/(4*pi*a) = 1.70534

Добавил проводок:

Цитата:

+ on(b5, u=1)

Результат:

Цитата:

capacitance/(4*pi*a) = 1.73401

Код можно протестировать онлайн на сайте FreeFem++ без скачивания и установки самой программы. Можно что-нибудь поменять, нарисовать чего-нибудь посложнее. Только надо следить чтоб радиус внешней сферы "rs" был достаточно велик и расчетная сетка была адекватной.

[LMA]

От греха подальше - конечный радиус проводка:

1. real a = 1; 
2. real c = 6*a; 
3. real rs = (c/2 + a)*4; 
4. real wr = a*0.1; 
5. border b1(t = wr, rs) {x = t; y = 0;}; 
6. border b2(t = 0, pi/2) {x = rs*cos(t); y = rs*sin(t);}; 
7. border b3(t = rs, c/2 + a) {x = 0; y = t;}; 
8. border b4(t = pi/2, -pi/2 + asin(wr/a)) {x = a*cos(t); y = c/2 + a*sin(t);}; 
9. border b5(t = c/2 - sqrt(a^2 - wr^2), 0) {x = wr; y = t;}; 
10.  
11. mesh Th = buildmesh(b1(10) + b2(10) + b3(10) + b4(10) + b5(5)); 
12. fespace Vh(Th, P2); 
13. Vh u, v; 
14.  
15. problem problem1(u, v) = int2d(Th) ((dx(u)*dx(v) + dy(u)*dy(v))*x) 
16.     + on(b4, u=1) + on(b2, u=0) + on(b5, u=1); 
17. for (int i = 0; i < 3; i++) 
18. { 
19.     problem1; 
20.     Th = adaptmesh(Th, u); 
21. }; 
22. problem1; 
23. plot(u, fill = true, value = true); 
24.  
25. real capacitance = int2d(Th) ((dx(u)*dx(u) + dy(u)*dy(u))*2*pi*x); 
26. capacitance = 1/(1/(2*capacitance) + 1/(4*pi*rs)); 
27. cout << "capacitance/(4*pi*a) = " << capacitance/(4*pi*a) << endl; 

Результат:

Цитата:

capacitance/(4*pi*a) = 1.7895

[shaxel]

Все было сделано как и планировалось. Будет 2-3 набора шаров.
Осталось оклеить их алюминиевой лентой.

[LMA]

Шары конечно красивые. shaxel, обратите ещё внимание на то, что наибольшая напряжённость поля может быть на перемычке (даже если это цилиндр). Меня смущает резьба.

[StaticZero]

Я смотрю на картинку и не могу взять в толк: почему перемычки квадратного сечения?

[shaxel]

Это не квадратная шпилька, просто она имеет одну шлифованную поверхность. Это надо для того, чтобы наклеить на плоскую поверхность распечатанную шкалу линейки, чтоб было понятно какое расстояние в данный момент между шарами... Угол раскрыва около 120-140 градусов.
LMA, я думал над этим вопросом. Тем не менее, я не считаю что на резьбе (острых выступах) перемычки будут пробои. Потому что перемычка находится именно в этом месте, между шарами. Обосновать это математически я не могу, но интуитивно я это понимаю.