Определение  .
. Граф называется связным, если любые две его вершины можно соединить путем.
Определение  .
. Компонента связности графа -- некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
Определение  .
. Компонентой связности называется класс эквивалентности относительно связности.
Определение  .
. Рассмотрим подграфы

графа

, порожденные множествами

, т.е. для

выполняется

. Так как любые две вершины из

связаны путем в

, то этот путь будет связывать их и в
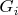
. Следовательно,
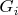
-- связный граф. Нетрудно проверить, что множества

образуют разбиение множества

(возможен случай

для некоторых

, в этом случае

-- тривиальный) и для графа

будет выполняться

-- дизъюнктное объединение графов

. При этом подграфы

называются компонентами связности графа

.
-- 26.07.2018, 20:03 --Перечитал много раз и понял, что у данного графа будет одна компонента связности. Правильно?
Почему то сначала мне захотелось разбить граф на подмножества попарных вершин и соответствующих ребер. Получилось три ребра и три отдельные вершины. Я это принял за компоненты.