Видимо, всё-таки не эквивалентно.
Ну, не знаю. У меня получилась такая конструкция. Пусть нам дан "диск". Его "краевая окружность" -- это

. Край ленточки -- это прямоугольник со сторонами

и

(пусть
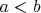
). Пусть вершины этого прямоугольника -- это точки

. Причем сторонам

соответствуют отрезки
![$[x, y], [z, w]$ $[x, y], [z, w]$](https://dxdy-04.korotkov.co.uk/f/3/b/1/3b1d7d2a9d572c6d153d79a242bb00fc82.png)
. Приклеим ленточку к диску сторонами

. Получим "диск с ленточкой" с двумя "краевыми окружностями" -- внешней и внутренней. Внешняя "краевая окружность" ограничена двумя кривыми, которые не пересекаются и соединяют точки (вершины)

. Внутренняя "краевая окружность" ограничена двумя кривыми между точками (вершинами)

. Таким образом диск с одной ленточкой, имеющий две краевые окружности эквивалентен мультиграфу с двумя компонентами связности, где в каждой компоненте ровно 2 вершины и 2 ребра. То есть диск (имеющий одну краевую окружность) эквивалентен связному (число компонент связности

) мультиграфу с 2 вершинами и 2 ребрами. Диск с одной ленточкой, имеющий две краевые окружности эквивалентен несвязному мультиграфу

, где каждая компонента содержит ровно 2 вершины и 2 ребра.
Ну, и теперь требуется доказать, что число краевых окружностей (равных числу компонент связности мультиграфа) диска с

ленточками не превосходит

. Это, как думаю, должно быть эквивалентно тому, что в мультиграфе

.