Найти интеграл (интересный имеет прикладное значение)

[Skipper]

Попробовал более простые варианты.

$\int\limits_{}^{} ( m ^ {-0.66 - (\ln m)} ) dm$

https://www.wolframalpha.com/input/?i=Integrate%5B+m%5E(-0.66+-+(Log%5Bm%5D)),%7Bm%7D%5D
Integrate[ m^(-0.66 - (Log[m])),{m}]

действительно не выражается в элементарных.

Однако если заменить 'минус' на умножить -

$\int\limits_{}^{} ( m ^ {-0.66 \cdot (\ln m)} ) dm$
Integrate[ m^(-0.66 * (Log[m])),{m}]

то интеграл берется, хотя и не в элементарных, но с помощью 'функции ошибок' Лапласа, $erf$

$-1.59323 erf(0.615457 - 0.812404 log(m)) + СConst $

а как она себя ведёт - известно.

Вот парадокс, операция 'минус' вместо 'умножить' - так усложняет функцию, что она не берется уже и с помощью
'функции ошибок' Лапласа.

[Skipper]

Я бы добавил новое понятие.
1) Есть "множество простейших элементарных функций".
2) Расширенное будет - "множество элементарных функций" - (содержит функции, которые есть - всевозможные сочетания, операции над множеством простейших элементарных функций).

3) Добавим "множество простейших определяемых функций".

содержит функции, которые есть - всевозможные сочетания, операции над множеством простейших элементарных функций + может содержать один интеграл.
Вот эта функция - и принадлежит к множеству простейших определяемых функций - т.к. мы её определили с помощью привлечения одного интеграла.

G(m) = $\int\limits_{0}^{m} ( a \cdot m ^ {-0.66 -0.001 \cdot m ^{1/3} \cdot (700 + \ln m)} ) dm$

4) Расширенное будет - "множество определяемых функций".
Функции которые выражаются операциями с конечным числом интегралов от элементарных функций.

И насколько я понимаю, все остальные функции, т.к. невозможно определить явно (можно только неявно - например в дифференциальном или функциональном уравнении, которое невозможно решить, сведя ответ к "множеству определяемых функций") - становятся автоматически невычислимыми.

В самом деле, рассмотрим какое-нибудь функциональное уравнение. Решить его не получается, т.е. нельзя найти явно функцию.
Следовательно, раз функция неизвестна, то невозможно даже численными методами (с помощью машины Тьюринга), найти, чему равно её значение в любых точках.

Существует ли теория, которая позволяет сказать - решается ли некое дифференциальное уравнение в виде "определяемой функции" ?

[Skipper]

Вот и глюк песочницы нашел

Plot[NIntegrate[0.0558 * w^(-1.55-0.001 w^(1/4)(1000 +Log[w])),{w,0,m}],{m,0.07,2.1},PlotRange->All]

выдает какую то ерунду. Должен быть график с ростом до 1.
так как этот же интеграл равен примерно 1.


https://www.wolframalpha.com/input/?i=Integrate%5B+0.0558+*+m%5E(-1.55-0.001+m%5E(1%2F4)(1000+%2BLog%5Bm%5D)),%7Bm,0.07,2.1%7D%5D

[arseniiv]

Skipper в сообщении #1303135 писал(а):

Существует ли теория, которая позволяет сказать - решается ли некое дифференциальное уравнение в виде "определяемой функции" ?

Может быть, дифференциальная теория Галуа.

Skipper в сообщении #1303169 писал(а):

выдает какую то ерунду

Не ерунду, а сообщение о том, что численное интегрирование сходится слишком медленно, конкретно в окрестностях нуля. И если менять нижний предел интегрирования с нуля на чуть бо́льшие значения, видно, что чем ближе к нулю, тем больше там набегает.

-- Ср апр 11, 2018 17:18:33 --

Вам следовало нижним пределом интегрирования вообще брать $0{,}07$ (как у $m$). Тогда будет вам та почти единица.

[Skipper]

Plot[NIntegrate[0.0558 * w^(-1.55-0.001 w^(1/4)(1000 +Log[w])),{w,0.07,m}],{m,0.07,2.1},PlotRange->All]

Так ?
Спасибо.
Только на wolframalpha.com он был посчитан и от нуля - т.к. площадь там ограничена (т.е. конечна).

[arseniiv]

Нет, не от нуля. Если приглядитесь к штрихам на оси абсцисс, увидите, что левый край области чуть меньше $0{,}1$.

-- Ср апр 11, 2018 18:50:36 --

Skipper в сообщении #1303198 писал(а):

Plot[NIntegrate[0.0558 * w^(-1.55-0.001 w^(1/4)(1000 +Log[w])),{w,0.07,m}],{m,0.07,2.1},PlotRange->All]

Так ?

Да. Кстати, в будущем окружайте небольшие куски кода типа этого тегами tt (как я сделал в цитате), лучше смотрится.

[wrest]

Skipper в сообщении #1303198 писал(а):

Только на wolframalpha.com он был посчитан и от нуля - т.к. площадь там ограничена (т.е. конечна).

Нет, теперь этот интеграл расходится, потому что вместо $-0,66$ вы поставили $-1,55$

Вы же в курсе что
$\int\limits_{0}^{x_0} x ^ {-a}dx$ расходится при $a\ge1$ ?

[Skipper]

wrest в сообщении #1303225 писал(а):

Skipper в сообщении #1303198 писал(а):

Только на wolframalpha.com он был посчитан и от нуля - т.к. площадь там ограничена (т.е. конечна).

Нет, теперь этот интеграл расходится, потому что вместо $-0,66$ вы поставили $-1,55$

Вы же в курсе что
$\int\limits_{0}^{x_0} x ^ {-a}dx$ расходится при $a\ge1$ ?

Я это понимаю так - $ x ^ {-a}dx$ при $a>0$ - график "прижимается" как к оси $X$, так и к оси $Y$.
Обе площади будут бесконечные, только в том случае, если $a=1$ .
Если $a>1$ - тогда бесконечна только площадь между осью $Y$, и графиком.
Если $a<1$ - тогда бесконечна только площадь между осью $X$, и графиком.

В данном случае, $a=1,55$, следовательно, бесконечна площадь между осью $Y$, и графиком.
А я хочу посчитать эту площадь, как определенный интеграл с диапазоном начиная от $0$.
На
https://www.wolframalpha.com/input/?i=Integrate%5B+m%5E(-1.55),%7Bm,0.1,1%7D%5D
он действительно график строит, но не считает сам интеграл (бесконечность должна быть).

Кстати, после более подробного анализа масс Вселенной, всё таки изменил функцию скорости накопления масс. Уточнённая она такая -

K(m) = ( a \cdot m ^ {-0.55 -0.0005 \cdot m ^{1/3} \cdot (1000 + \ln m)} ) dm$

Вот теперь уже окончательно, точно.
Сути не меняет - интеграл в любом случае неберущийся. Из этого распределения масс, последовало много интересных выводов,
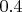
к примеру что среднестатистическая звезда в Галактиках примерно $0.4$ массы Солнца (т.е. если звездная масса нашей Галактики Млечный Путь
$80$ миллиардов солнечных, то всего звезд в галактике $200$ миллиардов). Ну и много других выводов. Построил теорию,
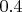
и описал многие вещи. (если все звёзды в Галактиках заменить звездой с $0.4$ массы Солнца - то масса Галактики останется прежней).
Ну и Солнце - это не такой уже и "карлик" - т.к. масса больше среднеарифметической.

А степень $-1.55 $ возникает (вместо $-0.55$) - если мы хотим перейти от функции скорости накопления масс -
к функции скорости накопления числа звезд и дозвёздных объектов - планеты, астероиды и т.д.

-- Чт апр 12, 2018 01:46:32 --

Цитата:

Может быть, дифференциальная теория Галуа.

Насколько я помню, читал раньше, что дифференциальная теория Галуа - позволяет определить, берущийся ли интеграл или нет.
Неужели с помощью этой теории, можно определить, можно ли вообще найти функцию - как решение дифференциального уравнения ?

Но можно и дифференциальное уравнение для этого не писать, я думаю, что можно написать обычное "функциональное уравнение",
такое, что невозможно будет найти функцию - её решение.
Т.е. это должна быть "функциональная теория Галуа", а не диференциальная. А построили такую?

[arseniiv]

Может, и построили, но класс произвольных функциональных уравнений уж очень широк, так что чтобы применить её, если она есть, вам всё равно наверняка придётся попотеть.

[wrest]

Skipper в сообщении #1303414 писал(а):

Я это понимаю так - $ x ^ {-a}dx$ при $a>0$ - график "прижимается" как к оси $X$, так и к оси $Y$.

Это не надо понимать как-то по своему, куда там чего прижимается, есть же четкие понятия "собственный" (proper) интеграл, "несобственный" (improper), "сходится" (converge), "расходится" (diverge) и т.п.

Skipper в сообщении #1303414 писал(а):

А степень $-1.55 $ возникает (вместо $-0.55$) - если мы хотим перейти от функции скорости накопления масс -
к функции скорости накопления числа звезд и дозвёздных объектов - планеты, астероиды и т.д.

Я хочу вам сказать, что если у вас интеграл расходится, то значит что-то пошло не так, и это надо как-то объяснить, ну типа что интеграл будем брать не от ровно нуля, а от почти нуля и объяснить чему и почему равно это "почти"

[Skipper]

Цитата:

Я хочу вам сказать, что если у вас интеграл расходится, то значит что-то пошло не так, и это надо как-то объяснить, ну типа что интеграл будем брать не от ровно нуля, а от почти нуля и объяснить чему и почему равно это "почти"

Да. "Почти от нуля", потому что минимальный объект во Вселенной, который можем считать - это атом водорода. А он имеет ненулевой размер.
Ну или если не нравится атом - тогда, к примеру Электрон+протон.
Но на таких масштабах функция уже неинтересна. Главная её особенность - показать распределение масс объектов, больших размеров нежели атомы водорода.

[wrest]

Skipper в сообщении #1303920 писал(а):

Главная её особенность - показать распределение масс объектов, больших размеров нежели атомы водорода.

А вы уверены что тогда

Skipper в сообщении #1303006 писал(а):

На долю планет, астероидов и т.д. космической пыли и межзвездного газа - приходится 36%.

У вас же там в солнечных массах считается? Атом водорода это примерно $10^{-60}$ солнечной. Подставьте

[Skipper]

Цитата:

На долю планет, астероидов и т.д. космической пыли и межзвездного газа - приходится 36%.

Нет, эту функцию я скорректировал, и стартовая степень там уже не $-0.66$, а $-0.55$. (Более подробно изучил
распределение количеств астероидов по массам, и звёзд ближайшего окружения по массам.)
А потому окончательно вышло,- На долю планет, астероидов и т.д. космической пыли и межзвездного газа - приходится 21%.
Разные исследователи по этой теме, получали разные оценки - от 10%, до 40%. А я нашел, самое точное распределение.

Вторая функция со степенью $-1.55$, показывает скорость роста именно количества объектов. Понятное дело, что её интеграл будет стремиться
к бесконечности, при параметре массы - стремящемся - к нулю. Т.к. атом водорода имеет ненулевой размер, то всё равно бесконечности не возникает.

Первая функция со степенью $-0.55$, показывает скорость роста именно - накопления масс. Её интеграл будет стремиться
к нулю, при параметре массы (объекта) - стремящемся к нулю. А потому, нам неважно, какое там количество малых объектов; интеграл - это все накопленные массы.
Берем к примеру интервал от $0$ до $0.001$ (масса Юпитера), и считаем, какую часть всей барионной массы составляют вся эта мелочь,
космическая пыль+астероиды+планеты, до массы Юпитера включительно.

Цитата:

Атом водорода это примерно $10^{-60}$ солнечной.

Погрешности на промежутке очень малых масс, если и будут, то незначительные.

Так вот, главное в мат-анализе, для человека, это не понимать легко, как взять те или иные неопределенные интегралы, причем в элементарных функциях,
закончили университет, все кто с этим по профессии не занимается - почти всё позабывали со временем.
А главное - понимать как построить нужные функции, и их интегралы, для решения тех или иных прикладных задач.
Если человек это умеет всегда по жизни, значит курс мат-анализа прошёл для него успешно.

[Skipper]

Короче.. Может действительно кому интересно -
http://www.astronomy.ru/forum/index.php ... 293.0.html

"Распределение барионных масс во Вселенной - Исследовательская работа"

Там и все эти функции по-своему отображаются. (просто так копи-паст не получится). Если же я сделал некую глобальную ошибку связанную с понимание мат-анализа, уточните. (Skipper_Norton там - это я, Skipper - на dxdy.ru)
Заранее, спасибо.

Вроде, всё сошлось, со многими экспериментальыми наблюдениями, и примерно такие же результаты, если сравнить с другими научными работами.

[arseniiv]

Запостите это в физику или астрономию — разделы, которые плотнее просматривают те, кому оно адресовано.