Определние угла манипулятора

[Dmitriy40]

А что, угол от вертикали уже определили? Двухосевым акселерометром? Вроде оба этих угла надо вычислять из показаний акселерометра, и примерно одинаковым способом (арккосинус и арктангенс).

Art_sh
Ни крен ни тангаж не являются углом от вертикали. Как бы акселерометр не крепили. В любом случае нужен пересчёт углов с датчика в углы манипулятора.

[Art_sh]

Вот такой вид система принимает, если добавить излучатель и приемник. Все расстояния между датчиками нам известны в любой момент времени.

[wrest]

Art_sh в сообщении #1232060 писал(а):

Все расстояния между датчиками нам известны в любой момент времени.

Тогда углы наклона прямой содержащей излучатели к плоскости содержащей приемники легко посчитать.

[Art_sh]

Чертежи, указаны все расстояния.
расстояния a,b,c,d - константы, задаются при установке сенсоров
расстояния e,f,g,h,i,j - измеряются аппаратно
необходимо определить углы α и β






Коммерческие обьявления на форуме давать нельзя, но за помощь отблагодарю))

[wrest]

Art_sh
Сразу предупреждаю: мне от вас ничего коммерческого не надо.
Формулы вы ищете сами, на свой страх и риск.

Помещаем начало координат в точку приемного сенсора где пересекаются отрезки $a$ и $b$
Направляем ось $Ox$ на перпендикулярно отрезку между оставшимися двумя сенсорами (отрезок обозначен как $c$)
Направляем ось $Oy$ параллельно отрезку $c$, так что положительное направление будет там, куда из начала координат растет отрезок $b$.
Направляем ось $Oz$ перепендикулярно плоскости $Oxy$ так что положительные значение будут там где излучатели.
Убеждаемся что получилась правая тройка $xyz$.
Обозначаем точки местонахождения сенсоров.
Тот, который в начале координат, обозначаем $O_1$, тот который на расстоянии $a$ от $O_1$, обозначаем $O_2$ и третий обозначаем $O_3$.

Координаты сенсоров обозначаем соответствующими тройками $x,y,z$ с индексами,
то есть $x_i,y_i,z_i$, где $i=1,2,3$

Тогда координаты сенсоров равны
Сенсора $O_1:$

$$x_1=0, y_1=0, z_1=0 \eqno(1)$$

Сенсора $O_2:$

$$x_2=k, y_2=-c/2, z_2=0 \eqno(2)$$

Сенсора $O_3:$

$$x_3=k, y_3=+c/2, z_3=0 \eqno(3)$$

Здесь $k$ - длина проекции отрезка $a$ на ось $Ox$
Исходя из того, что $a$=$b$ и треугольник $abc$ равнобедренный, по теореме Пифагора $k=\sqrt{a^2-(c/2)^2}$
Если этот треугольник НЕ равнобедренный (т.е. $a\neq b$, то надо в дальнейшие выкладки внести поправки).

Обозначим "верхний" излучатель, до которого расстояния $efg$ как $O_4$

Задача -- найти координаты $O_4$, которые обозначим как $x_4,y_4$ и $z_4$

Для нахождения координат $O_4$ нам нужно найти пересечение трех сфер с центрами $O_1,O_2$ и $O_3$ и радиусами $f$, $g$ и $e$ соответственно.

Записываем уравнения сфер
Сфера $O_1$:

$$f^2=(x-x_1)^2+(y-y_1)^2+(z-z_1)^2=x^2+y^2+z^2 \eqno(4)$$

Сфера $O_2$:

$$g^2=(x-x_2)^2+(y-y_2)^2+(z-z_2)^2=(x-k)^2+(y-c/2)^2+z^2 \eqno(5)$$

Сфера $O_3$:

$$e^2=(x-x_3)^2+(y-y_3)^2+(z-z_3)^2=(x-k)^2+(y+c/2)^2+z^2 \eqno(6)$$

Сможете решить систему уравнений (4)-(6) где $x,y,z$ - неизвестные, остальные буквы константы? Подсказка: начинайте с вычитания уравнения (5) из (6), найдёте $y$.

Когда решите, записывайте соответствующую систему уравнений для "нижнего" излучателя, обозначив его например $O_5$.

У вас получатся координаты двух точек $O_4$ и $O_5$

Следующий шаг: записать уравнение прямой, которая содержит точки $O_4$ и $O_5$

И наконец, зная уравнение прямой $O_4O_5$, вы сможете посчитать нужные вам углы.

[Art_sh]

to wrest:

Вам огромное спасибо за то, что нашли время и, главное, желание все это написать.

[wrest]

Art_sh
Ну, пока вы думаете над решением систем уравнений для определения координат излучателей, предположим что систему вы решили, и координаты теперь вам известны.
Пусть $O_4$ - "верхний" излучатель, с координатами $x_4,y_4$ и $z_4$, а $O_5$ - "нижний" излучатель, с координатами $x_5,y_5$ и $z_5$

Кстати, одной из проверок (в вашей программе) что в исходных данных нет противоречий, должно быть то, что $z_5<z_4$

Проведем вектор из $O_5$ в $O_4$, и назовем его $\vec{O_5O_4}$. Координаты вектора $\vec{O_5O_4}$ будут $x=x_4-x_5;y=y_4-y_5;z=z_4-z_5$, этот вектор называется "направляющий вектор"
Длина вектора $\vec{O_5O_4}$ находится по формуле $|\vec{O_5O_4}|=\sqrt{x^2+y^2+z^2}$
В этом месте, для подтверждения непротиворечивости показаний датчиков, вам надо убедиться что $|\vec{O_5O_4}|\approx d$ (т.е. что измеренное расстояние между излучателями соответствует реальному).
Найдем теперь единичный направляющий вектор для прямой $O_5O_4$ который назовём $\vec{m}$, его координаты будут
$m_x=\dfrac{x_4-x_5}{|\vec{O_5O_4}|}$, $m_y=\dfrac{y_4-y_5}{|\vec{O_5O_4}|}$, $m_z=\dfrac{z_4-z_5}{|\vec{O_5O_4}|}$
Координаты вектора $\vec{m}$ являются направляющими косинусами и равны косинусам углов, которые вектор $\vec{m}$ (и, конечно, $\vec{O_5O_4}$) образует с осями $Ox,Oy$ и $Oz$.

Можете сказать, как соотносятся эти углы с искомыми вами?

Для ещё одной проверки непротиворечивости показаний датчиков, я бы нашел точку пересечения прямой $O_5O_4$ с плоскостью датчиков $Oxy$ -- эта точка всегда должна попадать в какой-то круг допустимых значений (в этом круге манипулятор пересекается с плоскостью датчиков).

[Dmitriy40]

Написано всё правильно, но о сколько грабель остались незамеченными (неуказанными). Приведу некоторые из них, исключительно для Art_sh, чтобы не казалось что можно впрямую запрограммировать выведенные формулы и успокоиться. Проблемы связаны в основном с конечной точностью измерений расстояний.

wrest в сообщении #1232750 писал(а):

Кстати, одной из проверок (в вашей программе) что в исходных данных нет противоречий, должно быть то, что $z_5<z_4$

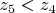
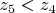
Ну, если проверка на положительность всех координат $z$ была сделана выше, при решении систем уравнений, то хорошо. Но, условие $z_5<z_4$ вполне может не выполняться для положений манипулятора вблизи плоскости датчиков, я бы так прикинул уже для углов порядка 5°-10° и меньше от горизонтали (зависит от соотшения $d$ и погрешности измерений).

wrest в сообщении #1232750 писал(а):

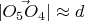
для подтверждения непротиворечивости показаний датчиков, вам надо убедиться что $|\vec{O_5O_4}|\approx d$ (т.е. что измеренное расстояние между излучателями соответствует реальному).

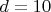
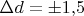
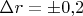
Снова, с какой точностью должно выполняться равенство? Априори неизвестно, надо думать/считать. В некоторых плохих случаях погрешность равенства может быть в несколько раз больше погрешности измерений, а для малых $d$ погрешность равенства может даже стать сравнимой с величиной $d$ (например $d=10$мм и $\Delta d = \pm 1{,}5$мм при погрешности измерений $\Delta r=\pm 0{,}2$мм).

wrest в сообщении #1232750 писал(а):

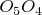
Для ещё одной проверки непротиворечивости показаний датчиков, я бы нашел точку пересечения прямой $O_5O_4$ с плоскостью датчиков $Oxy$ -- эта точка всегда должна попадать в какой-то круг допустимых значений (в этом круге манипулятор пересекается с плоскостью датчиков).

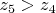
Тоже легко может не выполняться для положений манипулятора вблизи плоскости датчиков. Точка перечения может вообще уйти в противоположную сторону от датчиков (т.е. $z_5>z_4$). А если излучатели расположены достаточно далеко (в сравнении с величиной $d$) от центра шаровой опоры, то радиус круга пересечения может быть в десятки и сотни раз больше погрешности измерений расстояний - и его тоже надо аккуратно считать/оценивать, для лучшего и худшего случаев. Без такой оценки вообще малопонятно что именно брать за радиус этого круга, по какому критерию решать попала точка в круг или нет. И почему круг, а не эллипс с тем же азимутом большой оси?!

Вопрос азимутального угла в вертикальном положении вообще не рассмотрен.

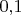
Ну про вопросы погрешности вычислений в этой задаче можно забыть, точности даже single арифметики вроде бы хватает за глаза. А вот к примеру точности целых типов, с шагом координат в погрешность измерений расстояния (например $0{,}1$мм) может и не хватить из-за округлений в процессе вычислений, надо брать шаг координат скажем в сотню раз меньше (думать хватит ли шага в десять раз меньшего мне лень, надо будет по конечным формулам прикидывать результирующую погрешность вычислений).

В итоге, пока остаёмся в рамках чистой математики с нулевой погрешностью - всё просто и замечательно. Когда запустим на практике - столкнёмся с кучей глюков, в процессе тестирования (что хорошо т.к. есть возможность поправить дело) или в работе у пользователя (что ужасно и может быть дорого во многих смыслах).

Повторю, я не отговариваю и не против, выкладки правильные, но вот как оно будет работать на практике - вопрос. Которым неплохо бы озадачиться ещё на стадии проектирования. Конечно если нет желания и времени потом долго доводить систему до ума разными костылями, например: трекингом перемещений излучателей; ограничением ускорений излучателей (сглаживанием/игнорированием рывков); установкой 4-го датчика вне плоскости первых трёх датчиков на сравнимом с $a, b, c$ расстоянии от первых трёх (могут быть проблемы с видимостью излучателей как раз в наиболее востребованной области положений манипулятора около плоскости первых трёх датчиков); программным повышением точности измерений.

(PS.)

Что-то чем дальше, тем больше оно напоминает не реальную задачу, а курсовуху. Формулы, в общем виде, расстояния "модельные" (круглые), игнор физических погрешностей (вибрация, стирание механики, скорость перемещений, нежёсткость конструкции, вопросы с калибровкой/поверкой, экранирование излучателей друг другом). Как-то всё оторвано от практики. Могу и ошибаться и все эти вопросы лишь оставлены на потом, когда будут идеальные формулы, но лично мне такой подход правильным не кажется.

[wrest]

Dmitriy40 в сообщении #1232757 писал(а):

Написано всё правильно, но о сколько грабель остались незамеченными (неуказанными).

Dmitriy40 в сообщении #1232757 писал(а):

В итоге, пока остаёмся в рамках чистой математики с нулевой погрешностью - всё просто и замечательно. Когда запустим на практике - столкнёмся с кучей глюков, в процессе тестирования (что хорошо т.к. есть возможность поправить дело) или в работе у пользователя (что ужасно и может быть дорого во многих смыслах).

Совершенно верно. После получения формул нужен их анализ на предмет погрешностей, это отдельная песня геморрой большая работа.

Но первый шаг -- всё равно математика (геометрия). Его все равно надо делать, по-любому.

Второй шаг -- это анализ погрешностей, который может внести коррективы, например, в расположение датчиков и излучателей.

Третий шаг -- моделирование с учетом подачи в алгоритм данных с погрешностями (распределенными по реальному закону распределения у реальных датчиков).

И, наконец, третий шаг -- натурные динамические испытания, которые покажут несоответствие ожиданий (расстояния известны точно и в любой момент) и реальности (есть задержка, данные от датчиков несинхронизированы, погрешность не такая как в паспорте на датчики и т.п.), которые надо учесть в модели :) Меня вот беспокоит то, что манипулятор существенно не тонкий и утверждение ТС о том, что "манипулятор не вращается вокруг собственной оси" -- я это утверждение понять не могу, потому что результат параллельного переноса по сфере зависит от траектории переноса, а значит нужен анализ что именно значит, что манипулятор "не вращается"...
Мне также непонятно почему место установки шаровой опоры известно неточно. Вернее, почему его нельзя измерить -- это явно добавило бы точности к определению углов. Подозреваю что просто-напросто должны быть чертежи манипулятора, на которых указаны точные размеры, но почему-то у ТС к ним нет доступа...

Так что вы совершенно правы, но решать-то что и как делать -- ТС-у...
Мы же не знаем -- может всё это ТС понимает и без нас, но у него была проблема именно с "идеальными" формулами.
А может, он пишет "курсач"...

[Art_sh]

Dmitriy40

это вполне реальная задача, не курсач)))
И вы правы, на данном этапе, на начальном, идет проверка базового алгоритма вычисления углов. Насчет чертежей, они есть, но если вы как то связаны с производством, то должны знать, что цифры в чертеже и реальные значения размеров довольно часто имеет посредственное отношение друг к другу, а так как я делаю только систему управления-навигации, то не могу отвечать за точность изготовления элементов конструкции. Именно поэтому вариант с добавлением нескольких сенсоров хорош тем, что позволяет уйти от конструкционных размеров, от люфтов и износа механики. Одно из условий, параллельность оси на которой находятся излучающие сенсоры к продольной оси манипулятора.
Манипулятор не может вращаться вокруг своей оси, поскольку на противоположной стороне от изл. сенсоров находится крепление для двух актуаторов. Их алгоритм работы - установка манипулятора на заданный угол по вертикале, установка угла по азимуту. При этом вертикальный угол минимальный 45гр - максимальный 90гр, по азимуту 0-75гр (150гр) от оси симметрии.

[wrest]

Art_sh в сообщении #1232777 писал(а):

Манипулятор не может вращаться вокруг своей оси, поскольку на противоположной стороне от изл. сенсоров находится крепление для двух актуаторов.

Манипулятор не может НЕ вращаться! :)
Возьмите карандаш между пальцев руки перпендикулярно ладони и представьте что предплечье это манипулятор, а локтевой сустав -- шаровая опора. И попробуйте подвигать "не вращая", понаблюдайте куда будет "смотреть" карандаш при разных способах движения к нужной комбинации углов. ;)

Хорошо, а если вы приварите длинный пруток перпендикулярно оси манипулятора вместо излучателя, наклоните манипулятор на 45 градусов по обоим углам, куда будет "смотреть" этот пруток? Можете пояснить картинкой? А лучше картинкой с приваренным прутком -- в 4-х экстремальных положениях манипулятора:
1. Углы по нулям (ну эт понятно -- манипулятор торчит вверх, пруток торчит параллельно основанию)
2. Первый угол ноль второй максимальный
3. Первый угол максимальный второй нулевой
4. Оба угла максимальные.

[Dmitriy40]

wrest в сообщении #1232763 писал(а):

Так что вы совершенно правы, но решать-то что и как делать -- ТС-у...

Несомненно. Но наша задача предупредить его что выписанные формулы - это ещё не полное решение практической задачи.
Да и писал то я для него.

Art_sh в сообщении #1232777 писал(а):

на данном этапе, на начальном, идет проверка базового алгоритма вычисления углов.

Ну, для проверки алгоритма конечные формулы и не нужны, достаточно доказательства единственности решения. Потом даже если прямые формулы вывести и не удастся (ну вдруг), то всегда можно решить задачу переборным или итерационным методом (да хоть табличным!). Т.е. Вы бежите немного впереди паровоза, сначала надо всё же определиться с конфигурацией сенсоров (в том числе учитывая и погрешности и физические ограничения), а потом уж выводить готовые формулы. Ну вот выше вывели (почти) итоговую формулу, а вдруг оказывается нужен 4-й датчик вне плоскости - и что делать? Снова менять все формулы ...
Да, если максимальный угол отклонения от вертикали не превышает 50°, то с тремя датчиками самые плохие случаи исключаются, где будет наибольшая погрешность что-то навскидку не вижу, вроде везде сферические слои пересекаются под большими углами (в смысле большие углы между радиусами или их продолжениеями) и погрешность всего раза в два больше погрешности измерений. Это если излучатели не уходят вверх на расстояние значительно большее $a, b, c$.

Art_sh в сообщении #1232777 писал(а):

не могу отвечать за точность изготовления элементов конструкции.

Потому и насторожило отсутствие упоминаний калибровки или поверки. Т.е. в программу задавать не цифры с конструкторского чертежа, а предусмотреть процедуру валидации этих чисел или измерения их в реальном изделии.

И кстати, если предусмотреть процедуру калибровки (однократную после изготовления или регулярную), то второй излучатель вообще говоря и не нужен. Можно выставить манипулятор вертикально (по определению!) и принять расстояния до датчиков за эталон. Если центр шаровой опоры находится где-то в плоскости датчиков - больше ничего знать и не нужно, его координаты вычисляются из координат излучателя (отбрасыванием координаты $z$, а $d=z$). Если не в плоскости - можно сделать ещё цикл измерений при точно известных углах отклонения (например 45° от вертикали (да транспортиром с отвесом измерить!) и 0° азимутально), по ним вычисляется положение центра сферы - т.е. центр шаровой опоры и расстояние от него до излучателя. И уже этих данных достаточно потом для вычислений углов манипулятора. И за счёт большего значения величины $d$ (которое будет от шаровой опоры до излучателя) точность определения углов будет выше.

Я хочу сказать что до полной постановки задачи выводить конечные формулы, даже для оценки погрешностей - лишнее. Достаточно определиться какие именно параметры системы необходимо знать чтобы получить нужный результат, а потом уж расписывать формулы до конца.

-- 11.07.2017, 16:44 --

Вопрос с валидацией конструктивных размеров тоже можно решить например калибровкой, измерять расстояния до датчиков (ими самими разумеется) из фиксированных положений манипулятора (например строго над одним из датчиков, строго посередине между ними, строго из центра треугольника датчиков, ещё каких).
Проводить не минимально необходимое количество измерений в разных положениях, а больше - и искать наиболее вероятные координаты всех датчиков и излучателей.
Добавить в конструкцию фиксированные упоры/ограничители (известно где) и при упирании манипулятора в них считать какие-то размеры/углы известными априори.
Да много можно вариантов придумать. И для каждого конечные формулы будут чуть разными.

[Art_sh]

Согласен, минимальное вращение есть

Центр шаровой опоры расположен ниже, чем центры сенсоров (расстояние измеряется от центра передающего сенсора до центра приемного).
Я понял, буду искать математика, который сможет сделать мат аппарат. Насчет калибровки, это обязательно будет.

[wrest]

Art_sh в сообщении #1232815 писал(а):

Согласен, минимальное вращение есть

Оно минимальное потому что у вас в анимации не 150х45 градусов, а меньше.

Art_sh в сообщении #1232815 писал(а):

Я понял, буду искать математика, который сможет сделать мат аппарат.

Это не математическая, а инженерная, механическая задача. Вам нужно искать инженера-механика.
Вся математика там укладывается в первый курс технического ВУЗ-а, ну может во второй (в части тервера). То есть нужен специалист по прикладной механике. Механизмы, проектирование механизмов, детали машин, регуляторы (автоматическое управление) -- вот это вот всё.

Математик вам не нужен, кмк.

[Dmitriy40]

Угол поворота в принципе можно определить расположив два излучателя по другому, несоосно манипулятору, например по его диаметру. Но вот точность этого угла из-за малой базы в поперечном сечении будет низкой.

И мне по прежнему кажется что сначала надо определиться с ресурсами (количество и расположение излучателей и приёмников, точность конструктивных расстояний, точность измерений, желаемая точность углов) и разделением задач между математикой, программой и технологичностью изготовления (что можно переложить на программу, что получить калибровкой, а что надо выводить математически строго). Пример с заменой второго излучателя на усложнение процедуры калибровки я приводил выше.

PS. Математик мог бы пригодится если строить модель манипулятора и теоретически искать/выводить её параметры (например погрешность по всей полусфере), причём именно что в общем случае, для произвольных размещений излучателей, датчиков и манипулятора. Но зачем такие глубины, проще нужно. И тогда да, инженера-механика за глаза хватит.