Поля остатков: пара вопросов начинающего

[kp9r4d]

Btw, есть ещё лекции Вавилова по алгебре (которые вы сами же несколько раз упоминали), почему бы вам их не посмотреть?

[vpb]

Ван дер Варден --- да, Алгебра. В принципе, вопрос не лишний, потому что он и по матстатистике писал, и по истории математики.

-- 30.03.2017, 16:10 --

А лекции Вавилова наиболее здоровЫ, думаю, для студентов Вавилова, которые с ним непосредственный контакт имеют. Для человека же не вполне в теме они могут оказаться даже вредны. Во всяком случае, очень уж они нетрадиционны. Вообще, есть такое наблюдение: чтоб плодотворно реализовывать нетривиальные педагогические идеи, и сам человек должен быть весьма неординарным (каковым Вавилов и является).

[Munin]

kp9r4d в сообщении #1204910 писал(а):

Любое поле можно расширить до поля, в котором любой многочлен будет распадаться на линейные множетели, это процедура алгебраического замыкания, правда алгебраическое замыкание конечного поля - всегда поле бесконечное.

Интересно! В перечисленных книгах (Лидл-Нидеррайтер и ван дер Варден) это есть?
Впрочем, после того, как стало ясно с квадратами, это уже "интуитивно ясно".
Осталось понять, интересны ли мне такие бесконечные поля, чтобы с ними тоже поиграть... :-)

vpb

vpb в сообщении #1204911 писал(а):

Ну вот, например, почему многочлен, с коэффициентами из поля, не может иметь больше корней, чем его степень.

Спасибо, кажется, я понял доказательство. Я правильно понимаю, что оно опирается на отсутствие делителей нуля, вот в этом пункте?

vpb в сообщении #1204911 писал(а):

Если $X=x$ --- корень для $f(X)$, отличный от $x_1$, то $x-x_1\ne0$, значит $f_1(x)=0$.

-- 30.03.2017 18:28:27 --

kp9r4d в сообщении #1204913 писал(а):

Btw, есть ещё лекции Вавилова по алгебре (которые вы сами же несколько раз упоминали), почему бы вам их не посмотреть?

Ага! Я попробовал! Как он начал вводить классификацию идеалов, так я и увяз!
Пока я понял из его лекций только одно: то, что в элементарной математике выражают как свойства отдельных элементов (делимость, простота, разложимость на множители), в суровой теории колец и полей выражают на языке свойств подколец и подполей. Но разобраться в этом пока пороху не хватает.

vpb в сообщении #1204915 писал(а):

Ван дер Варден --- да, Алгебра. В принципе, вопрос не лишний, потому что он и по матстатистике писал, и по истории математики.

Я просто там же нашёл его книгу "Современная алгебра" аж 1947 года издания - вряд ли то :-) И заманчивое название "Метод теории групп в квантовой механике" - впрочем, тоже вряд ли оно.

[kp9r4d]

Да везде есть, думаю. Есть ещё Винберг "Алгебра", сам по нему учился на первом курсе и знаю минимум двух человек, которые говорят, что учебник очень простой, доходчивый и понятный, а ещё и более современный (как минимум в том плане, что набран на Латехе и для глаза поэтому приятнее).

Ещё помню тут был пост с советами хороших 5-6 современных учебников по алгебре, разной степени простоты/сложности. Не прикрепленная, в которой ощущение, что есть названия всего, что смогли в gen.lib.rus.ec найти, а именно 5-6 хороших отобранных учебников; постараюсь сейчас вспомнить где это видел и кто этот пост писал.

А ещё, не мне вас учить как учиться, конечно, но я бы на вашем месте лекции из-за плохо запомненной классификации чего-то там не бросал. Сам Вавилов как раз придерживается той точки зрения, что в математике важна тональность, стиль, интенция, дух, чувство того, какие слова важные, а какие нет, то есть ощущение математики, как он говорил, на "мистическом уровне", а не на "фактическом". Поэтому - ну не запомнили какую-то классификацию, не поняли какой-то трюк в доказательстве - и ладно, запомните что-нибудь другое вместо этого. Вот например то, что утверждение о числах для $\mathbb{Z}$ можно по аналогии иногда переносить на утверждения о идеалах для любого коммутативного кольца - замечательная эвристика, очень хорошо, что вы её уловили.

[Munin]

kp9r4d в сообщении #1204990 писал(а):

Есть ещё Винберг "Алгебра"

Есть "Начала алгебры", есть "Курс алгебры", есть даже "Курс лекций по высшей алгебре" и "Лекции по алгебре. Первый курс, второй семестр" :-)
А просто "Алгебры" Либрусек не знает.

[kp9r4d]

Винберг "Курс алгебры", да.
Вот пост tolstopuz.

[g______d]

Munin в сообщении #1204971 писал(а):

Я просто там же нашёл его книгу "Современная алгебра" аж 1947 года издания - вряд ли то

Это название более старого издания "Алгебры".

[Munin]

kp9r4d в сообщении #1204990 писал(а):

но я бы на вашем месте лекции из-за плохо запомненной классификации чего-то там не бросал.

Если бы плохо запомненной! Хуже: плохо понятой. Не понятой вообще.
Лекции я бросать не собираюсь, но это место какое-то очень трудное. Или попробую его обойти, или вгрызаться... но это медленно.

kp9r4d в сообщении #1204990 писал(а):

утверждение о числах для $\mathbb{Z}$ можно по аналогии иногда переносить...

Там как раз проблема: школьные утверждения распадаются в иерархию вложенных систем, пользующихся и не пользующихся какими-то аксиомами, и для каждого утверждения надо заново выяснять, где оно справедливо, а где нет. И к тому же, запоминать массу новой информации. Многолетняя привычка легко и непринуждённо проводить выкладки над выражениями над $\mathbb{C}$ здесь как раз мешает: у $\mathbb{C}$ слишком много "хороших" свойств идут комплектом.

Ну, в общем, спасибо за сочувствие.

Я беру паузу на размышление и освоение книг. Пока мои вопросы отвечены. Да и вообще, мой интерес был мимолётным и неглубоким, увы.

-- 30.03.2017 19:32:41 --

kp9r4d в сообщении #1204996 писал(а):

Винберг "Курс алгебры", да.
Вот пост tolstopuz.

А, спасибо!

[vpb]

Munin
Совершенно верно, Вы правильно поняли, что используется отсутствие делителей нуля. А насчет что в математике важны интенция и дух ... неважно, в общем, как там коллега Вавилова цитирует. Позвольте повториться: Вавилов -- человек достаточно уникальный, и записи лекций Вавилова без самого Вавилова не очень полезны.

[kp9r4d]

(Оффтоп)

А я вполне убеждён, что математика не ограничивается аккуратными решениями нетривиальных задач. Более того, это даже не самая интересная и не самая определяющая её часть.

[AV_77]

Munin в сообщении #1204971 писал(а):

Интересно! В перечисленных книгах (Лидл-Нидеррайтер и ван дер Варден) это есть?

Лидл и Нидеррайтер только про конечные поля пишут, а все алгебраически замкнутые поля бесконечны. Так что там этого нет.

Ван дер Варден, конечно, уже несколько устарел, да и очень много готических символов использует. Еще очень не плохой учебник - С. Ленг, Алгебра. Из современных - Paolo Aluffi. Algrebra, Chapter 0. Правда это уже ближе к уровню аспирантуры.

[Sonic86]

Munin в сообщении #1204884 писал(а):

Sonic86 в сообщении #1204847 писал(а):

Мне был трудноват, м.б. Вам легче будет.

Да вы все издеваетесь??? У меня мозги уже заскорузлые, мне что попроще бы! Сразу же сказал! Мой уровень - научно-популярные лекции Савватеева на YouTube.

Эээ, ну я думал, раз Вы тензоры асилили...
Ну возьмите Айрленда Роузена Классическое введение в современную теорию чисел, или Бухштаба. Ну или Кострикина 3-й том, правда его я не читал, не знаю, насколько там все сложно.

Munin в сообщении #1204895 писал(а):

Что-то я не понял. Вот у меня $\mathbb{Z}_5,$ квадратный корень, я проверяю $2\mid 5-1,$ выполняется, и получаю, что корень должен извлекаться. Но из 1 и 4 он извлекается, а из 2 и 3 - нет.

Да, я - лошара
Попробую еще раз:
Мультипликативная группа конечного поля $\mathbb{Z}_p^\times$ (и даже $\mathbb{Z}_p^\times$) циклична, т.е. существует $g: \mathbb{Z}_p^\times=\{g^0, ..., g^{p-1}\}$, ее порядок $p-1$.
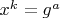
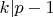
С учетом этого уравнение принимает вид $x^k = g^a$. Общий случай здесь сводится к двум крайностям: $k | p-1$ или $\gcd(k,p-1)=1$.
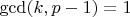
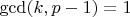
Если $\gcd(k,p-1)=1$, то можно возвести это уравнение в некую такую степень (находится алгоритмом Евклида), что получится равносильное уравнение $x=g^b$
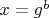
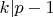
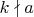
Если же $k | p-1$ ($k$ делит порядок группы), то тогда если $k\nmid a$, то решений вообще нет (возводим уравнение в степень $\frac{p^n-1}{k}$). Если же $k \mid a$, то есть $k$ корней.
А вообще это все избыточно: если группа $G=\mathbb{F}_{p^n}^{\times}$ циклична, то есть изоморфизм $\varphi$ (логарифм) ее в аддитивную группу: $\varphi(g^a)=a, \varphi(xy)\equiv x+y \pmod {p-1}, \varphi(\mathbb{Z}_p^{\times})=\mathbb{Z}_{p-1}^+$, а в аддитивной группе работать все-таки полегче: показательное уравнение $x^k=g^a$ в ней превращается в $k\varphi (x)=a\varphi(g) \pmod {p-1}$. И теперь здесь надо все коэффициенты с модулем сократить на НОД, потом проверить, есть ли общие делители у каких-либо коэффициентов (если есть, то сделать соотв-ий вывод), а если нет, то умножить на нужное число (которое опять же ищется алгоритмом Евклида) и получить решение.
Т.е. вышеприведенный критерий, который я пытался написать - это "подъем" критерия разрешимости линейных сравнений по составному модулю через "потенцирование".

(Оффтоп)

kp9r4d в сообщении #1204910 писал(а):

Чтобы проверить является ли $a$ квадратичным вычетом в $\mathbb{Z}_p$ есть эффективный вычислительный алгоритм - вычисление символа Якоби.

Зачем человека пугать? Символ Якоби для $\mathbb{Z}_p$ - это как раз символ Лежандра, да и вообще проще начать с критерия Эйлера

Munin в сообщении #1204895 писал(а):

А можно ли вообще, расширяя это поле до конечного, добиться того, чтобы извлекались все?

Не знаю. Где-то вспоминается как раз такое поле $\Omega$, но автор писал, что оно страшно устроено и все.

[warlock66613]

(Оффтоп)

Sonic86 в сообщении #1205036 писал(а):

раз Вы тензоры асилили...

Тензоры — ерунда, тензоры и я "осилил". Munin знает, что интеграл — это произведение цепи на коцепь — это посущественнее захудалых тензоров.

[Munin]

vpb в сообщении #1205024 писал(а):

Позвольте повториться: Вавилов -- человек достаточно уникальный, и записи лекций Вавилова без самого Вавилова не очень полезны.

Ну не знаю. Мне нравились. Может, даже упражнения возьмусь поделать.

И вообще, имхо, видеолекции - новый формат информации, который вполне ценен на своём месте.

AV_77 в сообщении #1205032 писал(а):

Еще очень не плохой учебник - С. Ленг, Алгебра. Из современных - Paolo Aluffi. Algrebra, Chapter 0. Правда это уже ближе к уровню аспирантуры.

Спасибо! (Ленг у меня есть.) Но вы совсем не смотрите, что я просил простой уровень! Вы меня закидываете, наоборот, сложным.

Sonic86 в сообщении #1205036 писал(а):

Эээ, ну я думал, раз Вы тензоры асилили...

Это не показатель! Мало ли чего я осилил в молодости, и с тех пор помню наизусть :-)

-- 30.03.2017 23:17:00 --

(Оффтоп)

warlock66613 в сообщении #1205082 писал(а):

Munin знает, что интеграл — это произведение цепи на коцепь — это посущественнее захудалых тензоров.

Это тоже из серии "освоишь в молодости - и дальше всю жизнь хвастаешься" :-)

[tolstopuz]

Munin в сообщении #1205101 писал(а):

Спасибо! (Ленг у меня есть.) Но вы совсем не смотрите, что я просил простой уровень! Вы меня закидываете, наоборот, сложным.

А почитайте действительно Айерленда-Роузена, хотя бы до квадратичных вычетов. Он как раз про вопросы из вашего стартового сообщения.