Рассматриваю поля остатков по модулю простых чисел

Интересуюсь конкретными примерами.
Возникли два таких вопроса:
1) всегда ли можно решить в таком поле (а) квадратное, (б) полиномиальное уравнение, и как его расширить, чтобы можно было?
2) как насчёт уравнения типа
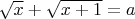
? Я тут выяснил, что оно легко сводится к квадратному, но в обычных числах.
Эти вопросы я задаю самому себе, и дальше такой поток мыслей (вопросы к окружающим - выделены жирным шрифтом).
Например, беру

Его таблица умножения такая:
Вижу, что квадратами являются только числа (0,) 1 и 4, то есть,

Добавляю

и соответственно, все линейные комбинации (все произведения выразимы в получившемся
![$\mathbb{Z}_5[\sqrt{2}],$ $\mathbb{Z}_5[\sqrt{2}],$](https://dxdy-02.korotkov.co.uk/f/5/e/b/5ebb388f6ed72ceb322c6c3f3cd175d682.png)
и даже все частные: в знаменателе можно избавиться от иррациональности). Получается двумерное векторное пространство, в котором
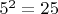
элементов.
Можно ли в этом
![$\mathbb{Z}_5[\sqrt{2}]$ $\mathbb{Z}_5[\sqrt{2}]$](https://dxdy-03.korotkov.co.uk/f/e/5/a/e5a0e965fdb3ee810a2faf2cf5153c1082.png)
извлечь корень из 3?
Обозначим за

корень многочлена

Тогда все элементы
![$\mathbb{Z}_5[\sqrt{2}]$ $\mathbb{Z}_5[\sqrt{2}]$](https://dxdy-03.korotkov.co.uk/f/e/5/a/e5a0e965fdb3ee810a2faf2cf5153c1082.png)
имеют вид

Посмотрим на их квадраты:
Чтобы получившееся число было

надо, чтобы
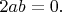
Правильно ли я понимаю, что в полях делителей нуля нет? Если бы были, то 


Правильно ли я понимаю, что  ?
?
Таким образом, имеем два случая:

и

Случай

мы уже знаем: это "действительные" числа, и их квадратами могут быть только 0, 1 или 4.
Случай

:

то есть,

Ура! В этом поле корень из 3 извлекается!
А извлекается ли корень из любого элемента? Как это проверить, не перебирая вручную все 25?
Каковы квадраты в других полях остатков?
Наблюдаем интересную картину: в квадраты попадает половина (ненулевых) остатков (исключением является
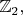
но оно малоинтересно, отброшу его в дальнейшем). Проверим это:
1) Не больше половины. Это очевидно:
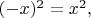
так что все противоположные элементы дают тот же квадрат. А противоположных ненулевых остатков ровно половина (

нечётное).
2) Не меньше половины. Вот это интересно. Допустим, квадраты совпадают:

Тогда
и мы имеем два случая: либо

либо
 Однако верно ли это?
Однако верно ли это? Возможный пробел я вижу в таком месте: многочлен

может раскладываться на множители более чем одним способом... Возможно ли это в полях? В полях остатков? (
По сути, я вообще ничего не доказал, а переформулировал вопрос в эквивалентный, и по-прежнему не знаю на него ответа.)
Если неквадратов половина, то верно ли, что мы можем научиться извлекать корни из любого "действительного" числа, добавив только корень из одного такого числа? Кажется верным. Пусть ниже

для некоторого

не являющегося квадратом. Тогда мы имеем даже "на мнимой оси" все числа вида

а их квадраты имеют вид

Достаточно, чтобы они не совпали с квадратом никакого третьего числа

чтобы тогда они заполнили всю половину неквадратов.


однако я снова упираюсь в вопрос:
можно ли смело раскладывать разность квадратов на множители, или это не равносильное преобразование в полях?----------------
Попробую извлечь корень 3-й степени из "действительного числа" в
![$\mathbb{Z}_5[\sqrt{2}].$ $\mathbb{Z}_5[\sqrt{2}].$](https://dxdy-04.korotkov.co.uk/f/7/6/e/76eef4bbab85b16dfb22657ed32991a982.png)
Для действительности нужно
Вроде, у нас получилось 3 кандидата, как и в

Но я ещё не проверил действительную часть. И ещё:
Нет ли ещё других решений?Уф, вопросы пока всё.