Решение парадокса лжеца (+ парадокс Рассела)

[ArshakA]

epros

epros в сообщении #1137223 писал(а):

Сформулируйте "исходную теорию".

mihaild в сообщении #1137251 писал(а):

Это есть даже в википедии

Две аксиомы:
1) $\forall x \forall y ( x=y \Longleftrightarrow \forall z (z \in x \Longleftrightarrow z \in y))$
2) Для каждой логической формулы $P(x)$ со свободной переменной: $ \exists y \forall x (x \in y \Longleftrightarrow P(x)) $

[arseniiv]

Во, прекрасно (за исключением того, что логические аксиомы тоже входят в теорию, а приведённое — лишь её собственные аксиомы; ладно, примем классическую логику). Теперь, во-первых, заметим, что раз у нас теория первого порядка, 2 — это не одна аксиома, а схема аксиом — по одной аксиоме для всех возможных формул $P(x)$ (вообще там ещё должно быть написано, что $y$ в этой формуле не свободна). В том числе аксиомой этой схемы будет $\exists y\forall x(x\in y\Leftrightarrow x\notin x)$. Теперь, пользуясь аксиомой 1, можно показать [тут пропущен формальный вывод], что $\exists!y\forall x(x\in y\Leftrightarrow x\notin x)$ (не только существует, но и единственно). Теперь можно ввести новую константу* $R$ и определение

$$\forall x(x\in R\Leftrightarrow x\notin x). \eqno{(R)}$$

И мы сразу же имеем $(R)\vdash R\in R\Leftrightarrow R\notin R$, что получается по правилу $\forall x\varphi\vdash\varphi[t/x]$, где $t$ — любой терм и $\varphi[t/x]$ — подстановка $t$ вместо всех свободных вхождений $x$ в $\varphi$.

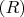
Итак, у нас на руках $R\in R\Leftrightarrow R\notin R$, и как отсюда выводятся одновременно и $R\in R$, и $R\notin R$, я уж писать не буду (с законом исключенного третьего это раз плюнуть, а если взять интуиционистскую логику, я не в курсе). Тогда они оба выводятся из $(R)$, так что аналогичные формулы без $R$** выводятся в нерасширенной этим определением теории без каких-либо гипотез. Теория противоречива.

* Можно, конечно, оставаться в нерасширенной теории без $R$, но это уж без меня.

** Например, перевод формулы $R\in R$: $\forall r(\forall x(x\in y\Leftrightarrow x\notin x)\Rightarrow r\in r)$. Правила перевода всегда есть там, где вводится расширение теории определением.

*** Надеюсь, комментарии не нужны и все умолчания покрываются предложенной литературой. (А что таить, там много где и предыдущее должно быть, и даже в большей строгости).

-- Пн июл 11, 2016 21:43:14 --

arseniiv в сообщении #1137274 писал(а):

Надеюсь, комментарии не нужны

Ибо перехожу в read-only.

[epros]

ArshakA в сообщении #1137262 писал(а):

Две аксиомы:
1) $\forall x \forall y ( x=y \Longleftrightarrow \forall z (z \in x \Longleftrightarrow z \in y))$
2) Для каждой логической формулы $P(x)$ со свободной переменной: $ \exists y \forall x (x \in y \Longleftrightarrow P(x)) $

Отлично, как Вам было выше сказано, из второй аксиомы выводится противоречие. Рассел показал как это сделать. Для этого нужно в качестве $P(x)$ взять $x \notin x$. Это свойство читается: "Множество $x$ не содержит само себя в качестве элемента". Рассел предложил называть множества, обладающие таким свойством, "ординарными".

-- Пн июл 11, 2016 20:57:37 --

arseniiv в сообщении #1137274 писал(а):

отсюда выводятся одновременно и $R\in R$, и $R\notin R$, я уж писать не буду (с законом исключенного третьего это раз плюнуть, а если взять интуиционистскую логику, я не в курсе)

Конструктивная логика никак не помешает выводу противоречия в данном случае, ибо закон исключённого третьего для этого не нужен.

Вообще, закон непротиворечия (часто путаемый с законом исключённого третьего) в несокращённой форме записывается как
$P \wedge (P \to \bot) \to \bot$
и в такой форме он работает даже в логиках без отрицания. Его даже не нужно отдельно закладывать в аксиоматику, ибо он выводится из одних только аксиом, определяющих связку $\wedge$, т.е. независимо от остальной аксиоматики.

Поэтому сей закон - святое, а всякыя посягательства на него - суть ересь.

[arseniiv]

epros в сообщении #1137275 писал(а):

Конструктивная логика никак не помешает выводу противоречия в данном случае, ибо закон исключённого третьего для этого не нужен.

Это-то я знаю, я просто не знаю (или не помню, или лень подумать) деталей вывода.

-- Пн июл 11, 2016 22:24:43 --

(Оффтоп)

epros в сообщении #1137275 писал(а):

Вообще, закон непротиворечия (часто путаемый с законом исключённого третьего) в несокращённой форме записывается как
$P \wedge (P \to \bot) \to \bot$
и в такой форме он работает даже в логиках без отрицания. Его даже не нужно отдельно закладывать в аксиоматику, ибо он выводится из одних только аксиом, определяющих связку $\wedge$, т.е. независимо от остальной аксиоматики.

Не могу ничего добавить кроме аналогии с теорией типов, где населённость $A\times(A\to0)\to0$ тоже до безобразия просто показывается, т. к. в соответствии с MP тут будет применение функции к аргументу, и пара из таких функции и аргумента нам и даётся на входе в искомой функции

$$\lambda(p\colon A\times(A\to0)).\mathsf{snd}(p)(\mathsf{fst}(p))\colon A\times(A\to0)\to0$$

(это только выглядит страшно — если не указывать типы, можно написать ерунду).

[ArshakA]

epros в сообщении #1137275 писал(а):

Отлично, как Вам было выше сказано, из второй аксиомы выводится противоречие. Рассел показал как это сделать.

Признаю. Разобрался в доказательстве arseniiv - оно безупречно. Но возник вопрос: почему когда было найдено противоречие его исправили именно отменной этих двух аксиом, а не модифицированием используемой логики. Ведь

arseniiv в сообщении #1137274 писал(а):

логические аксиомы тоже входят в теорию, а приведённое — лишь её собственные аксиомы

и поэтому остаётся не ясным зачем было переделывать такую понравившиюся всем, красивую и простую (по аксиматизации) теорию, когда можно было просто изменить её логические аксиомы. Я в самом начале говорил (не в смысле - так есть, а в смысле - так можно сделать), что некоторые элементы могут принадлежать всем, пренадлежать некоторым и не принадлежать никаким множествам ( Как множества могут содержать все (универсальное), содержать некоторые (обычное) и ни содержать ни каких (пустое) элементов).И в таком случае множество всех нормальных множеств не пренадлежат ни кому, а множество всех ненормальных множеств пренадлежит всем. То есть $ R \in R \Longleftrightarrow R \notin R $ не приведёт ни к каким противоречиям т.к. оба утверждения принимают одно логическое значение (ложь) , а не (как обязательно было бы в традиционной логике) разные.

[arseniiv]

ArshakA в сообщении #1137290 писал(а):

остаётся не ясным зачем было переделывать такую понравившиюся всем, красивую и простую (по аксиматизации) теорию, когда можно было просто изменить её логические аксиомы

Предлагаем варианты.

[epros]

ArshakA в сообщении #1137290 писал(а):

можно было просто изменить её логические аксиомы

Какие именно из логических аксиом Вам не угодили?

ArshakA в сообщении #1137290 писал(а):

$ R \in R \Longleftrightarrow R \notin R $ не приведёт ни к каким противоречиям т.к. оба утверждения принимают одно логическое значение (ложь)

Да уж, это сильно нетрадиционная логика. Каким образом может оказаться ложным то, что отрицает ложное утверждение? В конструктивной логике, которая не приемлет снятия двойного отрицания, это тоже немыслимо.

[ArshakA]

epros в сообщении #1137292 писал(а):

Какие именно из логических аксиом Вам не угодили?

$ x \in A \Longleftrightarrow x \notin \neg A $

epros в сообщении #1137292 писал(а):

Каким образом может оказаться ложным то, что отрицает ложное утверждение?

если $A$ - ложно, то $\neg A$ - истинно и ложным быть не может. Но при отмене вышеназванного соотношения, второе утверждение $(R \notin R)$ не будет отрицать первое $(R \in R$)

-- 11.07.2016, 21:18 --

epros в сообщении #1137292 писал(а):

В конструктивной логике, которая не приемлет снятия двойного отрицания

Вероятно это как раз то о чём я говорю. Двойное отрицание (инверсия множества и смена принадлежности на не принадлежность) - не снимается

[arseniiv]

ArshakA в сообщении #1137294 писал(а):

$ x \in A \Longleftrightarrow x \notin \neg A $

Вот тут путаница какая-то. У множеств нет отрицания. Что имелось в виду?

[epros]

ArshakA в сообщении #1137294 писал(а):

второе утверждение $(R \notin R)$ не будет отрицать первое $(R \in R)$

И тут путаница: $R \notin R$ по определению отрицает $R \in R$, ибо является сокращённой формой записи для $\neg R \in R$

[ArshakA]

arseniiv
имелась ввиду инверсия

[epros]

ArshakA в сообщении #1137299 писал(а):

имелась ввиду инверсия

Что это такое?

[ArshakA]

epros
Тогда иначе : утверждение $R \in R$ не отрицает утверждения $R \in \neg R$ (инверсия). Но так или иначе без $A \in A \Longleftrightarrow A \notin \neg A$ нельзя запереть множеству всех нормальных множеств не принадлежать ни себе ни множеству всех ненормальных множеств

[epros]

ArshakA в сообщении #1137303 писал(а):

$R \in \neg R$ (инверсия)

epros в сообщении #1137300 писал(а):

Что это такое?

[mihaild]

ArshakA, что такое $\neg R$, где $R$ - множество?