В формальных теориях типа арифметик нет средств для описания отношений.
Ерунду говорите. Причём тут теория множеств? Абсолютно ни при чём.
Во-первых, могут быть отношения, которые изначально есть в сигнатуре теории. Отношение равенства обычно есть в любой теории, и его часто включают в исчисление предикатов, чтобы не формулировать аксиомы равенства заново в каждой формальной теории. Содержательно равенство

означает, что

и

— "один и тот же объект" в том смысле, что во всех формулах можно заменять один из них другим без изменения значения истинности формулы.
Во-вторых, отношения можно определять в самой теории. Например, в арифметике Пеано неравенство

означает, что

, если мы не считаем

натуральным числом; если же натуральный ряд начинается с

, то

означает, что

, где штрих означает следующее натуральное число.
Что за отношение "

"? Что это такое?
Ну надо же! Человек смотрит на аксиомы арифметики и в упор не видит в них символа "

".
Я вот не понимаю, зачем мне там его искать? Аксиомы 1-5 приведены в самом начале темы.
Я говорил об арифметике первого порядка. У Вас же выписаны аксиомы теории второго порядка.
Вы как бы намекаете, что 1 не формула вовсе, и тогда 1-5 не может служить системой аксиом?
Видите ли, в теории второго порядка так написать можно, но даже в этом случае я в этом смысла не вижу. У Нечаева, на которого Вы ссылаетесь, есть аксиома

(сформулирована как часть аксиомы

) и сказано, что отсюда следует, что

. Я не возражаю, но смысла в этом также не вижу. Поясню подробнее.
Здесь также речь идёт о теории второго порядка. В арифметике второго порядка есть переменные двух типов. Один тип (строчные буквы) предназначен для обозначения натуральных чисел (или других объектов, если речь идёт не об арифметике), другой (прописные буквы) — для обозначения множеств натуральных чисел (или свойств, или предикатов; записывать высказывание "натуральное число

обладает свойством

" в виде

, или в виде
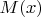
, или ещё как-то — дело вкуса и удобства). Поскольку буква

не может обозначать ничего, кроме натуральных чисел, писать

совершенно ни к чему. Поскольку символ (константа)

далее упоминается в аксиомах для натуральных чисел, он обозначает натуральное число, поэтому

не пусто. Но это рассуждение совершенно излишнее, поскольку теория предикатов обычно требует, чтобы предметная область была непустой, поэтому

уже в силу этого требования (Клини, § 17). Теория предикатов с пустой предметной областью рассматривалась, но ничего полезного там не обнаружилось, поэтому, во избежание ненужных проблем, лучше этот случай исключить заранее.
нет функции следования, а вместо нее прибавляется единица справа
Арифметику можно формализовать многими разными способами. Также существует много формальных теорий, в названии которых есть слово "арифметика".
необходимо разобраться ставить ли квантор в формуле


Куда его тут воткнуть? Тут ни одной переменной нет.
Конечно, формально мы имеем право написать эту аксиому в виде

, после чего кое-кто будет смотреть на нас с подозрением.
Знаете, может быть, не стоит что-то пытаться разобрать в теме, не освоив соответствующих prerequisites?