Две ракеты

[chislo_avogadro]

Skeptic в сообщении #1075389 писал(а):

Ракеты взлетят на одинаковую высоту.
Подсмотрено в учебнике физики для 8 класса.

Более "животворящего пенделя" невозможно себе представить!

[Dmitriy40]

Вероятно в учебнике для 8-го класса не учитывают уменьшение полной массы ракет из-за выработки топлива (на тот момент кажется ещё не знают ни логарифмы ни интегралы). А с таким условием решение становится простейшим из энергетических соображений.

[Skeptic]

Munin в сообщении #1075423 писал(а):

Тогда уж и точную ссылку давайте.

Munin, мне за вас даже как-то неудобно: у вас на книжной полке нет школьных учебников?, и вы не знаете, что в них написано?
А.В.Пёрышкин, В.В.Крауклис. Курс физики. Часть I. Учпедгиз - 1957 г.
Страницу сами найдёте, или подсказать?

[Theoristos]

Skeptic в сообщении #1075389 писал(а):

Ракеты взлетят на одинаковую высоту.
Подсмотрено в учебнике физики для 8 класса.

(Оффтоп)

Учебник новый? Высота небесной тверди?

[Pphantom]

Skeptic в сообщении #1075472 писал(а):

Munin, мне за вас даже как-то неудобно: у вас на книжной полке нет школьных учебников?, и вы не знаете, что в них написано?
А.В.Пёрышкин, В.В.Крауклис. Курс физики. Часть I. Учпедгиз - 1957 г.
Страницу сами найдёте, или подсказать?

Skeptic - замечание за демагогию.

[Munin]

Skeptic в сообщении #1075472 писал(а):

Munin, мне за вас даже как-то неудобно: у вас на книжной полке нет школьных учебников?, и вы не знаете, что в них написано?

У меня их слишком много, и я не знаю, что в них написано во всех.

Skeptic в сообщении #1075472 писал(а):

Страницу сами найдёте, или подсказать?

Раз я спросил точную ссылку, то и давайте точную ссылку. Не заставляйте всех окружающих пролистывать учебник от корки до корки.

[slavav]

Dmitriy40 в сообщении #1075435 писал(а):

Вероятно в учебнике для 8-го класса не учитывают уменьшение полной массы ракет из-за выработки топлива (на тот момент кажется ещё не знают ни логарифмы ни интегралы). А с таким условием решение становится простейшим из энергетических соображений.

Вы ошибаетесь, задача решается одинаково при любой динамике ракет. Это кинематическая задача.

Пример: пусть ускорение свободного падения $g = 10$. Не будем учитывать изменение массы ракет (мы в восьмом классе), реактивное ускорение примем постоянным $a = 20$. Глубина обрыва 15 метров. Время работы двигателей 3 секунды.

Считаем по секундам (время, скорость и высота первой ракеты, скорость и высота второй ракеты):

t  v1 h1   v2  h2
0   0  0    0   0
1  10  5  -30 -15
1  10  5   30 -15 (момент отскока, скорость второй ракеты изменила знак)
2  20 20   40  20
3  30 45   50  65

На третьей секунде вторая ракета выше и движется быстрее.

[dovlato]

Мне захотелось понять, что приходит на смену интегралу энергии, когда и масса ракеты меняется, и её двигатель работает.
Пусть $u(t), s(t)$ - это, соответственно, та скорость и то перемещение, которое были бы у ракеты в условиях невесомости. Это - её заданные исходные характеристики.
Тогда, как нетрудно показать, исходное уравнение её движения в дифференциалах таково:

$$d(v-u)+gdt=0$$

Его интеграл

$$v-u+gt=C$$

Здесь $v$ - скорость ракеты в поле тяготения. За плюс принято направление вверх. Величина С зависит от начальных условий.
Умножим исходное ДУ на $v-u$; при этом учтём, что $vdt=dy, udt=ds$, где $y(t)$ - высота ракеты:

$$(v-u)d(v-u)+g(dy-ds)=0$$

То есть

$$d\left[\frac{(v-u)^2}2+g(y-s)\right]=0$$

Таким образом, получаем эквивалент того самого "энергетического" интеграла движения

$$\frac{(v-u)^2}2+g(y-s)=C$$

В дальнейшем простоты ради будем считать, что ракета достигает максимальной высоты $y_m$, когда её двигатель уже не работает, а "реактивная скорость" $u$ принимает своё максимальное значение $u_m$.
Итак, 1-я ракета, стартующая сразу вверх.
Она достигает максимальной высоты в некоторый момент $t_1$, когда $v=0$. Заметим, что в интеграле для скорости, очевидно, С=0. Положив в нём $v=0, u=u_m$ получим, что момент достижения наивысшей точки равен

$$t_1=\frac{u_m}{g}$$

В интеграле движения первой ракеты константа C, как нетрудно видеть, также равна нулю. Отсюда получаем максимальную высоту для неё

$$y_{1m}=s(t_1)-\frac{u_m^2}{2g}$$

Теперь - 2-я ракета.
В качестве независимого параметра удобнее принять не высоту обрыва $H$, а $t_0$ - то время, которое ракета летит вниз.
Нетрудно видеть, что в момент удара внизу она успевает набрать скорость

$$v_0=u(t_0)+gt_0$$

При этом глубина равна

$$H=s(t_0)+g\frac{t_0^2}2$$

Для $t\ge t_0$ интеграл для скорости имеет вид

$$v-u+gt=2gt_0$$

Отсюда, полагая $v=0, u=u_m$, получим, что наивысшая точка достигается второй ракетой в момент

$$t_2=2t_0+\frac{u_m}{g}$$

То есть

$$t_2=t_1+2t_0$$

Интеграл движения (для $t>t_0$) имеет вид

$$\frac{(v-u)^2}2+g(y-s)=-2gs(t_0)$$

Это нетрудно проверить, положив $v=v_0, y=-H$. Снова полагая $v=0, u=u_m$, получим, что наибольшая высота полёта второй ракеты равна

$$y_{2m}=s(t_2)-2s(t_0)-\frac{u_m^2}{2g}$$

Разность наибольших высот 2й и 1й ракет равна

$$\Delta y=y_{2m}-y_{1m}=s(t_1+2t_0)-2s(t_0)-s(t_1)$$

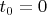
Проанализируем. Легко видеть, что при $t_0=0$ будем иметь $\Delta y=0$, как и должно быть (учитываем, что $s(0)=0$). Возьмём производную от этой разности по $t_0$:

$$\frac{d\Delta y}{dt}=2[u(t_1+2t_0)-u(t_0)]=2[u_m-u(t_0)]$$

Она, очевидно, неотрицательна; она строго положительна, если $u(t_0)<u_m$.

$$\Delta y=2\int_0^{t_0}[u_m-u(t)]dt>0$$

Таким образом, $\Delta y(t_0)$ есть строго возрастающая функция при достаточно малых $t_0$, а далее она выходит на константу (естественно, положительную).
Подозреваю, что тот же результат ( т.е. $y_{2m}>y_{1m}$) будет верен вообще при всех физически осуществимых режимах полёта.

[slavav]

dovlato в сообщении #1075538 писал(а):

Мне захотелось понять, что приходит на смену интегралу энергии, когда и масса ракеты меняется, и её двигатель работает.

Согласен с вашим решением. Но одно замечание: вы избегаете энергии так как боитесь криков беотийцев? Если это единственная причина, тогда вы не обязаны рассматривать энергию всей ракеты. Рассмотрите как меняется энергия заклёпки в корпусе ракеты (полезного груза, всего корпуса ракеты и т.п.) под воздействием внешних сил. Для неё/него действует закон сохранения энергии, можно вычислить работу внешних сил и показать что к заклёпке второй ракеты всегда подводится большая мощность, а значит и взлетит эта заклёпка выше.

[dovlato]

slavav в сообщении #1075546 писал(а):

dovlato в сообщении #1075538 писал(а):

Мне захотелось понять, что приходит на смену интегралу энергии, когда и масса ракеты меняется, и её двигатель работает.

Согласен с вашим решением. Но одно замечание: вы избегаете энергии так как боитесь криков беотийцев? Если это единственная причина, тогда вы не обязаны рассматривать энергию всей ракеты. Рассмотрите как меняется энергия заклёпки в корпусе ракеты (полезного груза, всего корпуса ракеты и т.п.) под воздействием внешних сил. Для неё/него действует закон сохранения энергии, можно вычислить работу внешних сил и показать что к заклёпке второй ракеты всегда подводится большая мощность, а значит и взлетит эта заклёпка выше.

Нет, здесь нет беотийцев)). Любопытства ради, можете заглянуть на форум "Вашего репетитора", с которым я длительное время плодотворно сотрудничаю.
Но зато если заглянете в тамошний политический раздел - получите такую "освежающую" струю..
А здесь я сам для себя захотел исследовать, насколько далеко удастся продвинуться, оставаясь в строгих формальных рамках.
С заклёпкой - думаю так же, как Вы говорите. А что, ведь хорошая задача!

[slavav]

dovlato в сообщении #1075547 писал(а):

А что, ведь хорошая задача!

+1

[Xey]

Чтобы развеять таинственность, надо бы упомянуть , что энергия топлива переходит в энергию корпуса ракеты и в энергию газов. Рассматриваемый маневр меняет соотношение этих энергий.
Туман наводит U образный отражатель, с космическим маневром заморочек было бы меньше.

[Утундрий]

Xey в сообщении #1075554 писал(а):

Туман наводит U образный отражатель, с космическим маневром заморочек было бы меньше.

По сути это и есть гравитационный манёвр. Туман наводит неумение мыслить космически. Не научились ещё (с)

[bondkim137]

slavav в сообщении #1075546 писал(а):

заклёпки в корпусе ракеты (полезного груза, всего корпуса ракеты и т.п.)

(Оффтоп)

я обозвал это болванкой. но если заклепкой вам нравится больше, не возражаю =)

[Gleb1964]

Вторая ракета, которая делает U-образный маневр, взлетит выше, ответ очевидный и без массы формул.

Утундрий в сообщении #1075563 писал(а):

По сути это и есть гравитационный манёвр.

Читал тему и думал, кто вспомнит про гравитационный маневр? Тратить рабочее тело для ракеты выгоднее в потенциальной яме, чем глубже, тем выгоднее - у отработанного рабочего тела останеться меньше энергии, зато больше достанется ракете. Наибольшую выгоду вторая ракета получит, если истратить все рабочее тело коротким импульсом в нижней части U-образной связки (замаскированный перицентр орбиты в задаче).