С помощью определения предела последовательности показать,

[Elliot]

что данная последовательность $x=2n/(1+n^2)$ при $n\to\infty $ имеет своим пределом число А=0. Найти целое значение N, начиная с которого |x-А|$< $$\varepsilon$
$\varepsilon=10^\left\lbrace-1\right\rbrace$
Решение:
$|2n/(1+n^2)|$ $< $$\varepsilon$
$2n/(1+n^2)$ $<$ $\varepsilon$
$\varepsilon$+$\varepsilon$$\cdot$$n^2$$<2n$
n$>$$(\varepsilon$+$\varepsilon$$\cdot$$n^2)$$/2$

Помогите, пожалуйста. Битый час не могу понять, что делать дальше.

[provincialka]

1) Записать аккуратно формулы (Карантин не дремлет! Вместе с модераторами).
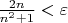
Например, наведите мышку на эту формулу: $\frac{2n}{n^2+1}<\varepsilon$ И отдельныеи буквы заключите в доллары.

2) Решить полученное квадратное неравенство либо предварительной оценкой свести его к линейному.

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

Elliot
Наберите все формулы и термы $\TeX$ом. Каждая формула и терм должны быть заключены в одну пару долларов, никаких других долларов внутри формулы не нужно.
Каждая формула целиком заключается в одну пару долларов, внутри формул никаких долларов не нужно.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.