Симметричные кортежи из последовательных простых чисел

[DemISdx]

Попробую не много по другому объяснить под катом:

(Оффтоп)

Yadryara в сообщении #1694042 писал(а):

А в чём разница? Я имею в виду здесь, в о25, не в SPT.

В SPT использовалась программа primesieve автора Kim Walisch.

Да. В качестве поставщика простых и только.

Цитата:

В о25 она не использовалась.

Да.

Цитата:

В SPT использовалась компиляция исходного кода.

Да.

Цитата:

В о25 она не использовалась.

Нет.

Цитата:

Потому что PARI/gp это интерпретатор.

Да.

Цитата:

То есть код один.

Нет.

Цитата:

В данном случае, в o25 нет кода скрипта как части кода приложения.

Нет.

Цитата:

Потому что код скрипта и есть код приложения.

Нет.

Цитата:

Правильно понимаю?

Елси подойти к попытке понимания поднятого Вами вопроса совсем по другому.

Что имею ввиду?
Например: запуск пари/гп в ворде.
Сначала кажется, что это бред (пари/гп в ворде. Ха-ха! два раза.).

Но, на самом деле, в ворде есть VBA (visual basic application).
API (https://ru.wikipedia.org/wiki/API) которого совершенно спокойно позволяет запустить другую внешнюю программу, хоть пари/гп.

Т.о. да - в ворде можно написать некий код обвязки на бейсике, который будет запускать пари/гп, это первый момент.
Управляемость приложения пари/гп с запущенным в нем скриптом - будет почти никакая, это второй момент.

Упомянутый "код обвязки" это и есть то, что связывает одну программу с другой.
Замените слово "ворд" на слово "боинк" и получится примерно тоже самое.

Подытожывая:
1. исходники "боинк" публикуются официально, т.е. - есть.
2. скрипт пари/гп один какой-то - есть.
3. "код обвязки" - нет.

Т.о. повторить исполнение невозможно.
Но это не наша с Вами головная боль.
Мне лично на это - по барабану.
Ответственность на авторе проекта.
Даже если на это с предметом...

[Yadryara]

Спасибо, Демис.

А между тем, ошибки в этом проекте пошли уже вопиющие. https://boinc.mak.termit.me:5000/algo_15/

И обе 13-ки продублированы. И что, никто не замечает? Смотрим сюда:

Цитата:

4378373698229277981631: [0,12,42,60,66,90,96,102,126,132,150,180,192]
13028061663376234999921: [0,12,42,60,66,90,96,102,126,132,150,180,192]

И сразу же, вплотную, идёт пост:

Цитата:

4378373698229277981631: [0,12,42,60,66,90,96,102,126,132,150,180,192]
13028061663376234999921: [0,12,42,60,66,90,96,102,126,132,150,180,192]
57585961039768749672481: [0,12,42,60,66,90,96,102,126,132,150,180,192]
98825206244343167433241: [0,12,42,60,66,90,96,102,126,132,150,180,192]

Мало того, что один и тот же паттерн зачем-то повторяется, так ещё и кортежи одни и те же плюсуются. Как этого можно не замечать??

И никто даже не замечает, что аж целая сотня 11-к продублирована???

Сравните списки 1 и 2 за два последних дня.

Лишь бы похвастаться огромным количеством 11-к, которое получено сложением одних и тех же кортежей

[DemISdx]

Yadryara в сообщении #1694256 писал(а):

ошибки в этом проекте

Ошибки как были, так и останутся.
Наверное такое было ТЗ при запуске.

Yadryara в сообщении #1694256 писал(а):

Как этого можно не замечать

Думаю, что это просто повторно опубликовано на форуме.

Yadryara в сообщении #1694256 писал(а):

аж целая сотня 11-к продублирована???

Мы ТЗ не знаем, возможно это цель.

Yadryara в сообщении #1694256 писал(а):

за два последних дня

Не смотрю уже давно.
Не интересно.
Не уверен, что зимние ошибки были исправлены.
Не особо занимательно следить за глупостью.

Yadryara в сообщении #1694256 писал(а):

Лишь бы похвастаться

А разве когда-то было иначе???
Найти несколько 13-ток за три дня?
Это наверное фетиш такой.
Мы такие значения просто пропускали, насколько я помню.
Как не интересные, с математической точки зрения.
Валились-то они сотнями в час...
Их потом - что? Солить что-ли?
Выкинуть и все...

[Yadryara]

Демис, ошибки уже частично признаны, но об этом позже.

Вчера поступила отличная новость: со второй попытки наконец-то посчитался паттерн с рекордным для своих длины и диаметра количеством формул.

Yadryara в сообщении #1686740 писал(а):

Казалось бы, судя по предыдущему увеличению для одинаковых диаметров, время будет в 3-4 раза больше, но по прогрессу похоже что будет 4-хзначное количество часов.

Всё-таки худший прогноз не сбылся: в 4.4 раза — 914 часов.

Паттерн       Формул     k1        Время    k2

21-372-53        2.1                42 h
21-372-11       19.7    9.5        100 h   2.4

21-384-10        1.4                60 h   
21-384-15        8.8    6.2        105 h   1.7

21-396-111       1.6                90 h
21-396-34       17.5   11.2        166 h   1.8

21-408-114       1.4               144 h
21-408-79       21.5   15.4        316 h   2.2

21-420-1179      1.04              208 h
21-420-762      31.0   30.0        914 h   4.4

Обсчёт проведу позже и представлю выводы. Это затрудняется ещё и тем, что я не все страницы полностью вижу.

[Yadryara]

Ну вот покажу данные для минимаксных пар всех обсчитанных паттернов 21-к.

Да, чтобы хорошо увидеть, что последний считавшийся паттерн, для которого больше всего формул из всех 48 обсчитанных, всё-таки не на первом, а на 2-м месте по матожиданию (прогнозу), пришлось считать для периода $0-97\#$.

№    Паттерн                        Прогноз по HL1, штук         Норм.        Лёгкость
                                                 0 - 97#        формул          поиска

              Конс. max  8         9        10        11

1.   21-324-1       252103    246966    247837    247837         2.435          101778
2.   21-324-2       696560    684352    686382    686088         6.575          104353

5.   21-336-3       110223    106396    107077    106783         1.186           90050
10.  21-336-8       405275    390519    393197    392903         4.297           91432

13.  21-348-1       131689    123121    124756    124461         1.575           79023

23.  21-360-10       77896     70059     71623     71329         1.000           71329
32.  21-360-19      713844    627269    644929    644635         9.402           68565

39.  21-372-53      148663    117028    123925    122605         2.072           59176
40.  21-372-11     1399604   1068514   1141401   1127315        19.744           57097

41.  21-384-10       99896     66539     74225     72667         1.410           51545
42.  21-384-15      638010    383248    443713    431071         8.811           48924

43.  21-396-111     113604     64905     76511     74077         1.569           47218
44.  21-396-34     1300882    660183    816292    782775        17.535           44640

45.  21-408-114     113362     38944     57860     53624         1.395           38453
46.  21-408-79     1707158    660609    924650    865916        21.504           40268

47.  21-420-1179    101224     16649     39383     33987         1.036           32808
48.  21-420-762    3070872    476879   1175988   1009636        31.046           32521

Так что именно эти два паттерна с диаметрами 372 и 420 самые перспективные для поиска 21-ки и на периоде $0-73\#$.

Если получше понять как ведёт себя лёгкость поиска, научиться её считать поточнее, то вместо утомительного многочасового счёта констант, можно будет получать прогноз просто умножая лёгкость на нормализованное количество формул.

[Yadryara]

Yadryara в сообщении #1694288 писал(а):

Если получше понять как ведёт себя лёгкость поиска, научиться её считать поточнее, то вместо утомительного многочасового счёта констант, можно будет получать прогноз просто умножая лёгкость на нормализованное количество формул.

Озадачился этим вопросом. Честно посчитал все представленные паттерны 11-к аж по 25-ю константу, что конечно избыточно — и ненулевых констант порой меньше и сходится до тысячных.

Используется синтаксис Text

№     Паттерн      Прогноз по HL1, штук         Норм.       Лёгкость   Средняя
                   C25          0 - 47#        формул         поиска   лёгкость

1.   11-132-1                     10847         2.500           4339     
2.   11-132-2                     11356         2.667           4258     4299

3.   11-144-1                     13169         4.167           3161     
4.   11-144-2                      6934         2.083           3328     
5.   11-144-3                     10361         3.333           3108 
6.   11-144-4                      8545         2.667           3204     3200

7.   11-156-1                      6159         2.500           2463  
8.   11-156-2                      9992         4.000           2498  
9.   11-156-3                      8289         3.333           2487  
10.  11-156-4                     11588         4.667           2483  
11.  11-156-5                      7589         3.000           2530     2492

12.  11-168-1                      2949         1.750           1685    
13.  11-168-2                      5458         2.917           1871    
14.  11-168-3                      2530         1.333           1898    
15.  11-168-4                      9914         5.333           1859    
16.  11-168-5                      2291         1.250           1833    
17.  11-168-6                      7326         4.000           1831    
18.  11-168-7                      5521         2.917           1893    
19.  11-168-8                      5107         2.667           1915    
20.  11-168-9                      3784         2.000           1892     
21.  11-168-10                     5258         2.917           1803     1848

22.  11-180-1                      3766         2.963           1271     
23.  11-180-2                      6890         5.556           1240     
24.  11-180-3                      8396         6.667           1259     
25.  11-180-4                      9491         7.407           1281     
26.  11-180-5                      5666         4.444           1275     
27.  11-180-6                     10749         8.333           1290     
28.  11-180-7                      1770         1.389           1275     
29.  11-180-8                      2831         2.222           1274     
30.  11-180-9                      7131         5.556           1284   
31.  11-180-10                     2205         1.620           1361  
32.  11-180-11                     3888         2.778           1400  
33.  11-180-12                     3644         2.778           1312  
34.  11-180-13                     3665         2.917           1257  
35.  11-180-14                     6016         4.667           1289  
36.  11-180-15                     4406         3.333           1322  
37.  11-180-16                    13286        10.000           1329  
38.  11-180-17                     6757         5.000           1351  
39.  11-180-18                     4622         3.556           1300  
40.  11-180-19                     5343         4.000           1336  
41.  11-180-20                     6242         4.667           1337  
42.  11-180-21                     4643         3.500           1327  
43.  11-180-22                     6060         4.667           1299  
44.  11-180-23                    12390         9.333           1327  
45.  11-180-24                     8500         6.222           1366  
46.  11-180-25                    10836         8.000           1355  
47.  11-180-26                     5089         3.889           1309  
48.  11-180-27                     4991         3.889           1283  
49.  11-180-28                     5665         4.167           1360  
50.  11-180-29                     8917         6.667           1338  
51.  11-180-30                     7070         5.333           1326  
52.  11-180-31                     9709         7.500           1295  
53.  11-180-32                     8835         6.667           1325  
54.  11-180-33                     8247         6.222           1325  
55.  11-180-34                     3245         2.500           1298  
56.  11-180-35                     1393         1.000           1393  
57.  11-180-36                     6416         4.667           1375     1315
                     Сумма =     383735.316

4299 / 3200 = 1.343
3200 / 2492 = 1.284
2492 / 1848 = 1.348
1848 / 1315 = 1.405
 

Падение средней лёгкости есть. Но как она себя ведёт, кроме того что неуклонно падает, пока непонятно. Как ведут себя отдельные паттерны, тоже не шибко понятно. Да, кучкуются вокруг среднего, с погрешностью до 8%.

[Yadryara]

Посчитал для 9-к побольше паттернов для 8 различных длин. Картина несколько прояснилась:

Используется синтаксис Text

№     Паттерн      Прогноз по HL1, штук         Норм.       Лёгкость   Средняя
                   C20          0 - 41#        формул         поиска   лёгкость

1.   9-84-1                       5424         1.000           5424     5424

2.   9-96-1                       5546         1.500           3697     3697

3.   9-108-1                      5372         2.000           2686     2686

4.   9-120-1                      3206         1.800           1781     1781
5.   9-120-2                      6963         3.750           1857     1819
6.   9-120-3                      3574         1.875           1906     1848
7.   9-120-4                      2397         1.250           1917     1865
8.   9-120-5                      3570         1.875           1904     1873
9.   9-120-6                      3875         2.000           1938     1884
10.  9-120-7                      2621         1.500           1748     1864

11.  9-132-1                      2861         2.400           1192     1192
12.  9-132-2                      4353         3.600           1209     1201
13.  9-132-3                      2922         2.500           1169     1190
14.  9-132-4                      4613         3.750           1230     1200
15.  9-132-5                      2449         2.000           1224     1205
16.  9-132-6                      3593         3.000           1198     1204
17.  9-132-7                      3720         3.000           1240     1209
18.  9-132-8                      3041         2.500           1216     1210

19.  9-144-1                      2928         3.600            813     813
20.  9-144-2                      3491         4.500            776     795
21.  9-144-3                      2341         3.000            780     790
22.  9-144-4                      2990         3.750            797     792
23.  9-144-5                      2042         2.500            817     797
24.  9-144-6                      2347         3.000            782     794
25.  9-144-7                      1742         2.250            774     791
26.  9-144-8                      1039         1.200            866     801
27.  9-144-9                      1693         1.875            903     812
28.  9-144-10                     1158         1.500            772     808
29.  9-144-11                     2631         3.000            877     814
30.  9-144-12                      910         1.200            758     810
31.  9-144-13                     1004         1.250            803     809

32.  9-156-1                      1007         1.800            560     560
33.  9-156-2                      1434         2.500            574     567
34.  9-156-3                      1705         3.000            568     567
35.  9-156-4                      1283         2.250            570     568
36.  9-156-5                      2062         3.600            573     569
37.  9-156-6                      2174         3.750            580     571
38.  9-156-7                      1211         2.143            565     570
39.  9-156-8                      2650         4.571            580     571
40.  9-156-9                      1664         2.857            582     572
41.  9-156-10                     1173         2.000            586     574
42.  9-156-11                     1764         3.000            588     575
43.  9-156-12                     1773         3.000            591     576
44.  9-156-13                     2391         4.000            598     578
45.  9-156-14                     1776         3.000            592     579

46.  9-168-1                      1051         2.743            383     383
47.  9-168-2                       988         2.500            395     389
48.  9-168-3                       917         2.400            382     387
49.  9-168-4                      1551         4.000            388     387
50.  9-168-5                      1745         4.500            388     387
51.  9-168-6                      1044         2.743            381     386
52.  9-168-7                      1399         3.429            408     389
53.  9-168-8                      1005         2.500            402     391
54.  9-168-9                      1491         3.750            398     392
55.  9-168-10                      962         2.400            401     393
56.  9-168-11                     1203         3.000            401     393
57.  9-168-12                      602         1.600            376     392
58.  9-168-13                      849         2.057            413     393
59.  9-168-14                      406         1.000            406     394
60.  9-168-15                     1168         3.000            389     394
61.  9-168-16                      490         1.200            408     395
62.  9-168-17                     1206         3.000            402     395
63.  9-168-18                     1132         2.743            413     396
64.  9-168-19                      660         1.714            385     396
65.  9-168-20                      863         2.057            419     397
66.  9-168-21                      789         2.057            383     396
67.  9-168-22                     1535         3.600            426     398
68.  9-168-23                      615         1.500            410     398
                                144152.335

5424 / 3697 = 1.47
3697 / 2686 = 1.38
2686 / 1864 = 1.44
1864 / 1210 = 1.54
1210 /  809 = 1.50
 809 /  579 = 1.40
 579 /  398 = 1.45

(5424 / 398) ^ (1/7) = 1.452
 

Ну то есть, видимо, для бо́льших диаметров лёгкость так и будет падать примерно в 1.45 раза.

И этот кэф, как видно, падает с ростом длины. Для 11-к он пока (4299 / 1315) ^ (1/4) = 1.34. А для 21-к ещё заметно меньше.

То есть для бо́льших длин, в том числе для 21-к, 23-к и т. д. количество формул будет играть всё бо́льшую роль (мы уже видели 31-кратное), а диаметр — всё меньшую роль.

Попробую посчитать и другие длины.

[Yadryara]

И опять тишина.

Yadryara в сообщении #1694522 писал(а):

Попробую посчитать и другие длины.

7-ки пока посчитал, все диаметры по 156. То есть 9 диаметров: с 60 до 156 включительно. Оказалось я зря не учитывал пока интервал, а кэф от него зависит.

Покажу только квинтэссенцию. Как и раньше делю соседние средние лёгкости друг на друга, а затем считаю среднее геометрическое.

Используется синтаксис Text

7-ki        0 -- 37#
69877 / 44548 = 1.57
44548 / 29224 = 1.52
29224 / 19130 = 1.53
19130 / 12654 = 1.51
12654 /  8049 = 1.57
 8049 /  4888 = 1.65
 4888 /  3001 = 1.63
 3001 /  2038 = 1.47

(69877 / 2038) ^ (1/8) = 1.556


7-ki           0 -- 41#
1391371 / 940423 = 1.48
 940423 / 651500 = 1.44
 651500 / 450940 = 1.44
 450940 / 314860 = 1.43
 314860 / 212426 = 1.48
 212426 / 137704 = 1.54
 137704 /  90107 = 1.53
  90107 /  64391 = 1.40

(1391371 / 64391) ^ (1/8) = 1.468
 

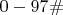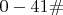И для этого же интервала $0-41\#$ показатель для 9-к был 1.452, почти такой же как и для 7-к.

Вывод: надо брать период побольше и считать по HL1 матожидания для кортежей, которые удаётся посчитать за недолгое время.

Ещё заметил, что неровности (которые, видимо, зависят от паттернов) сохраняются для разных периодов. Например, это большие значения 1.65 и 1.54 на третьих с конца строчках.

[DemISdx]

Yadryara в сообщении #1694564 писал(а):

И опять тишина.

Ну я просто Вас читаю.
Мне этого пока достаточно.

(Оффтоп)

Зачем мне лезть в Ваши формулы или их формирование?
Ответ очевиден - не зачем.

Вчера глянул немного стату по новому приложению ТС.
Из нового, только побыстрее считаются задачи. И это хорошо.
В прочем об этом Вы уже писали.
Глянул на ошибки - ну все тоже самое творится...
Т.е. мой тезис здесь ранее:

DemISdx в сообщении #1694266 писал(а):

Ошибки как были, так и останутся.
Наверное такое было ТЗ при запуске.

Подтверждается.
Т.е. других изменений, в лучшую сторону, нет, а в худшую - похоже есть.
Зачем мне постить повторно то, о чем уже неоднократно описано и не только мной?