sergei1961Почему, признак Дирихле в чистом виде: если суммы
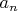
ограничены, а
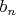
монотонно стремится к нулю, то ряд

сходится.
РустВы говорили о нижней оценке при

. Она не получается из Ваших рассуждений.
Я оцениваю не сумму синусов, а сумму экспонент. Сумма синусов для одного самого большого может равняться и нулю, но взяв еще один такой интервал или несколько (если это позволяется) за счет сдвигов фаз выходим на величину порядка

и для синусов.
Цитата:
Откуда Вы берете верхнюю оценку мне тоже неясно. На мой взгляд, без каких-то дополнительных сведений о

она не должна получаться.
Оценка сверху получаются из разложения интервала (0,n) на полные подинтервалы и тем, что сумма на высшем уровне оценивается как константа на корень от длины, а на низших ступенях из-за того, что их сумма на каждом уровне меньше чем

, где

максимально возможное значение суммы на уровне

, соответственно сумма по всем уровням меньше

, оценивается только высшим уровнем с точностью до константного множителя.
Если все аккуратно расписать, то получается, что сумма

всегда остается величиной порядка

. Константы

зависят от а, но при заданном а всегда
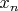
блуждает в некотором кольце.
Цитата:
Это неверно. У Харди и Литтлвуда доказано, что существуют иррациональные

, при которых нельзя получить оценку лучше

.
.
Скорее всего вы путаете. Легко показать, что для любого N существует а и

, такие, что сумма не меньше N, но это не значит, что при фиксированном отличным от нуля а, сумма будет вести себя так для бесконечного числа n.