Объясните, пожалуйста, суть парадокса квантовой запутанности

[warlock66613]

chislo_avogadro в сообщении #998178 писал(а):

После этого вторая частица обретает волновую функцию и становится известен базис, в котором надо её мерять, чтобы получить совершенно определённый результат.

Никакой волновой функции вторая частица не обретает. Волновая функция остаётся одна на две частицы. Но базис такой становится известен (точнее мы сами его выбираем первым измерением. В этом базисе суперпозиции, конечно, не будет.

[chislo_avogadro]

schoolboy в сообщении #998213 писал(а):

это корреляция за счет передачи энергии

Какую передачу энергии Вы имеете ввиду? Будете соображать с ответом, поясните, почему этот ответ не подойдёт и для квантового случая.

-- 30.03.2015, 22:29 --

warlock66613 в сообщении #998224 писал(а):

Никакой волновой функции вторая частица не обретает. Волновая функция остаётся одна на две частицы.

А если это два фотона? Один исчез при измерении, что остаётся?
Пусть имеем
${| \psi(A,B) \rangle}= \frac{1}{\sqrt{2}}\{{| \uparrow_A \rangle}{| \downarrow_B \rangle} - {| \downarrow_A \rangle}{| \uparrow_B \rangle}\}
Измерение частицы $B$ дало: $\downarrow$.
Можем сказать, что волновая функция ещё не измеренной частицы $A$ есть $| \uparrow_A \rangle$?

[Munin]

schoolboy в сообщении #998093 писал(а):

Так у себя - то он может менять ось.

Ось - да. Но этим не меняется ни вектор состояния (когда он есть), ни матрица плотности (когда его нет), а только базис, на который они проецируются.

schoolboy в сообщении #998093 писал(а):

Разумеется, в любом случае, то, что он своими действиями изменяет то, что происходит у другого, может наблюдать либо третья сторона или он же, изучая лабораторный журнал.

Может - и ничего не пронаблюдает. Хоть обызмеряйтесь, все распределения вероятностей у другого будут теми же самыми, независимо от действий первого.

schoolboy в сообщении #998104 писал(а):

Еще раз. Ключевое здесь отличие от носков и волчков – ЛЮБОЕ направление.

Нет, ключевое отличие в другом, и жаль, что вы на это закрываете глаза.

Tim в сообщении #998169 писал(а):

Если определить состояние - интерференции не будет.

Вот тут ошибка.

-- 30.03.2015 22:39:09 --

chislo_avogadro в сообщении #998225 писал(а):

А если это два фотона? Один исчез при измерении, что остаётся?

Да хоспади, научитесь вы этой элементарной технике вычислений с бра-кет векторами, хотя бы по ФЛФ. И сами всё посчитать сможете.

[chislo_avogadro]

Munin я там уже подправил Кстати, ваше мнение по вопросу?

[warlock66613]

chislo_avogadro в сообщении #998225 писал(а):

Можем сказать, что волновая функция ещё не измеренной частицы $A$ есть $| \uparrow_A \rangle$?

Ну, поскольку в такой постановке фолновая функция факторизуется, то да - можем.

[Tim]

Munin в сообщении #998235 писал(а):

Tim в сообщении #998169 писал(а):

Если определить состояние - интерференции не будет.

Вот тут ошибка.

Не понимаю, простите. Как может частица интерферировать сама с собой, если её состояние определено? Ну например мы определили, через которую из щелей прошел электрон.

[Cos(x-pi/2)]

schoolboy

Давайте доразбираем приведённый Вами пример (простой и хороший) до конца (только у меня опять цейтнот, увы; поэтому пишу кратко). Чтобы не возиться с числами "1/2", пусть речь идёт о знаках проекций спина. Т.е. пусть $s_1$ это делённая на 1/2 проекция спина электрона на ось 1, измеряемая наблюдателем 1; она принимает значения $+1$ или $-1.$ Аналогично: $s_2$ со значениями $+1$ или $-1$ характеризует проекцию спина второго электрона на ось 2, измеряемую наблюдателем 2.


1) Легко вычислить по правилам КМ (упражнение), что среднее значение произведения $s_1s_2$ есть

$ \langle s_1s_2 \rangle = -\cos (\alpha)$ ,

где $\alpha$ - угол между осями 1 и 2. Достаточно рассматривать значения этого угла от $0$ до $\pi.$

Спрашивается, а что такого "квантово запутанного" есть в этом ответе? Ведь в данном примере - с синглетным спиновым состоянием пары электронов - источник каждый раз испускает пару электронов с равной нулю суммарной проекцией спина на одну и ту же ось.

Очевидно, уже сам этот закон сохранения должен привести к жёсткой корреляции измеряемых проекций спина на одну и ту же ось: при $\alpha = 0$ наблюдатели в каждом измерении с достоверностью будут получать $s_2 = - s_1,$ поскольку вследствие заведомо нулевой суммарной проекции спина должно быть $s_1+s_2=0.$ Этот факт не зависит от выбора направления оси, пока она единая для обоих наблюдателей. Так что, при $\alpha = 0$ (а Вы, имхо, только на этот случай и нацеливаете внимание) с очевидностью имеем: $\langle s_1s_2\rangle = s_1s_2 = -1.$

Аналогично, по той же причине при $\alpha = \pi$ с очевидностью имеем: $\langle s_1s_2\rangle = s_1s_2 = +1.$

Оба этих ответа даёт и формула $-\cos(\alpha),$ так что "квантовость" здесь ещё не проявляется, а проявляется только закон сохранения суммарной проекции спина. Следовательно, весь интерес-то для нас будет только в случаях, когда оси наблюдателей 1 и 2 составляют угол $\alpha,$ отличный от $0$ и $\pi.$


2) Поэтому для сравнения рассмотрим какую-нибудь классическую модель с таким же законом сохранения суммарного момента импульса. Пусть вместо электронов источник каждый раз испускает пару классических волчков, вращающихся в противоположные стороны вокруг одной оси. Пусть её направление каждый раз случайное, с равномерным распределением вероятности в полном телесном угле $4\pi.$

Детекторы же пусть работают так. Направлению детектора 1 соответствуют две полусферы с телесными углами по $2\pi$ каждая: одна окружает положительную полуось 1, а другая отрицательную; плоскость, разделяющая полусферы, перпендикулярна к оси 1. Если направление оси вращения волчка попало попало в положительную полусферу детектора, то детектор выдаст $s_1=+1,$ а если в отрицательную, то $s_1=-1.$

Короче говоря, всё просто: если проекция оси вращения волчка на ось детектора 1 положительная, то $s_1=+1,$ а если в отрицательная, то $s_1=-1.$ О полусферах речь ради наглядности: чтобы было ясно, что вероятность для оси волчка оказаться в телесном угле $\Omega$ равна $\Omega/4\pi,$ и что вероятностью волчка быть перепендикулярным к оси детектора можно пренебречь как мерой нуль. Для второго детектора всё аналогично.

В этой простой модели при изменении угла между осями детекторов от $0$ до $\pi$ легко вычислить (упражнение), что:

${\langle s_1s_2 \rangle}_{\text{class}}=-1+\dfrac{2\alpha}{\pi}$ .

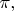
Как видим, при угле $\alpha$ между детекторами, равном $0$ или $\pi,$ в классической модели получаются те же значения коррелятора -1 и +1, как и в квантовой механике; и объясняется это тривиальным образом - тем, что эта корреляция порождена ещё в источнике: условием нулевого суммарного момента импульса испускаемых частиц .

"Kвантовая запутанность" в данном примере проявляется только в том, что квантовый коррелятор зависит от угла между детекторами как $-\cos(\alpha),$ т.е. не так, как в классической модели. Вот из этого косинуса далее уже можно вывести более выразительные следствия: нарушение неравенств, выполняющихся в классической модели (упражнение).

В упомянутой выше классической модели скрытыми параметрами являются сами векторы момента импульса волчков: они существуют у волчков сразу же после акта испускания волчков источником. У квантовых же электронов направление спина до измерения не просто не известно наблюдателю, а вообще не может быть введено в теорию; электрон характеризуются только средним по ансамблю вектором спина, но никак не индивидуальным вектором спина. Это отличие от волчка и ведёт к квантовой специфике корреляционных функций для электронов сверх той, что следует просто из законов сохранения.

(P.S. наверное на форуме всё это уже где-то было. Если так, то прошу извинить, поленился провести "поиск".)

[Tim]

Свободная частица - ${| \psi \rangle}_1 = \sum_a A_a {| a \rangle_1}.$

Спутанная, когда произвели измерение одной из них ${| \psi \rangle}_1 = \sum_a \Phi_{ab'} {| a \rangle}_1$ .

Чем отличается ${| \psi \rangle}_1 = \sum_a A_a {| a \rangle_1}.$ от ${| \psi \rangle}_1 = \sum_a \Phi_{ab'} {| a \rangle}_1$
Можно ли их различить, и почему нет?

[schoolboy]

Cos(x-pi/2)

Большое спасибо за подробный анализ, в частности, за изобретение остроумного детектора с полусферами. Пока тоже в цейтноте и детально всё не обдумал (не сделал упражнения на неравенства Белла). Но чуть позже посчитаю и вообще как следует подумаю о вашей конструкции.

[schoolboy]

Cos(x-pi/2) в сообщении #998286 писал(а):

У квантовых же электронов направление спина до измерения не просто не известно наблюдателю, а вообще не может быть введено в теорию; электрон характеризуются только средним по ансамблю вектором спина, но никак не индивидуальным вектором спина. Это отличие от волчка и ведёт к квантовой специфике корреляционных функций для электронов сверх той, что следует просто из законов сохранения.

Я несколько иначе про это скажу. Дальше будет много слов (думать некогда), но, может, кто-нибудь прочитает.

1. Суть эффекта запутанных частиц в том, что действие на одну из них мгновенно отражается на другой, как удалена она бы не была. Это демонстрирует нелокальность квантовой физики.

2. Если мы возьмем два фермиона в синглетном состоянии и измерим проекцию у одного на направление, то фактически мы произведем измерение над всей системой. Измерение в квантовой механике (по крайней мере в этом случае) изменяет систему, она ориентируется вдоль направления, поэтому второе измерение ( в другой лаборатории) ничего не даёт, поскольку это измерение в этом же базисе.

3. В классических системах результаты могут быть похожи, например два противоположно закрученных волчка. Но разница в том, что измерение не изменяет их, их закрученность создается в момент создания системы и не изменяется.

4. Я пытался различить квантовый и классический случаи произвольным выбором направления. Я предположил, что квантовый случай для любого направления даст одинаковый результат (поскольку измерение разворачивает систему в этом направлении), а для классического результата - нет, например, для направления, перпендикулярного оси волчков измерение ничего хорошего не даст. Cos(x-pi/2) похерил эту мою гениальную по простоте примитивную идею, придумав детектор, в котором состояние, в котором направление измерения, перпендикулярное оси волчков, не наблюдаемо.

5. Но и при придуманном детекторе классический и квантовый случай различаются анализом корреляционных функций. То есть при втором измерении (во второй лаборатории) надо поворачивать направление относительно первой лаборатории. В квантовом случае первое измерение поворачивает систему (точнее ориентирует вдоль направления), а во второй лаборатории, повернув направление, мы измеряем эту повернутую (ориентированную) систему в новом базисе (появляется косинус поворота). В классическом случае мы делаем два измерения одной и той же системы в одном и том же состоянии, но в разных направлениях.

[vlapay]

Может быть кто-то из знающих людей прояснит ещё один момент по этой теме. Читал, но так до конца и не понял, что успех теории скрытых параметров зависит от эффективности детектора, что, если кпд регистрации меньше чем $1/\sqrt 2$, то тогда можно обойтись без нелокальности. Непонятно, как именно можно это сделать. Если это какие-то "умные" детекторы, которые помнят, что и как они измеряли, то ведь можно использовать всё время новые детекторы, после каждого импульса?

[Munin]

schoolboy в сообщении #998623 писал(а):

1. Суть эффекта запутанных частиц в том, что действие на одну из них мгновенно отражается на другой, как удалена она бы не была. Это демонстрирует нелокальность квантовой физики.

Надо понимать смысл этого "отражается". Матрица плотности не меняется.

[Geen]

Извиняюсь, дурацкий вопрос, а запутанность - это да/нет или от 0 до 1?

[Munin]

Можно обсуждать и то и другое. Если вектор состояния составной системы не факторизуется - то запутанность есть. Но можно измерить его отличие от ближайшего разложения на множители.

[Geen]

(Оффтоп)

Munin в сообщении #998723 писал(а):

Но можно измерить его отличие от ближайшего разложения на множители.

А как, кстати?