То есть, что происходит. Во-первых, мы сокращаем углы вдвое, и переходим от эллипса вокруг фокуса к эллипсу вокруг центра. Во-вторых, мы переходим от времени

ко времени
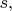
которое идёт медленнее в апоцентре, и быстрее в перицентре, и в результате делает "равномернее" движение точки по эллипсу. И в итоге, получаем вместо кеплеровского эллипса осцилляторный. Так?
Я, право, не знаю, что получается по-отдельности в результате этих переходов, но
совокупный эффект этих преобразований в невозмущенном случае дает гармонический осциллятор, решение которого

, где константы

определяются начальными данными. Фиктивным временем

преобразования Сундмана является
эксцентрическая аномалия, т.е. угол, который составляет с положительным направлением оси перицентра направление на точку некоторой окружности
с центром в центре исходного кеплеровского эллипса. В результате преобразования Леви-Чивиты не только углы сокращаются вдвое, но и расстояния

уменьшаются до

, потому что берется корень

. Вот из-за этого корня и появляется двойка в знаменателе.
В пространстве же в некотором смысле возникает аналог этого корня. Было замечание
Ну вот почему бы не выбрать знаки в четвёртой строке так, чтоб получился кватернион, а? Красивенько будет.

Выбор такой матрицы, какую я написал, приводит к уравнению гармонических осцилляций. Если выбрать знаки так, чтобы получилась при перемножении с вектором в результате единичка (это имелось ввиду?), то не факт, что уравнения дадут гармонический осциллятор и вообще будут регуляризированы и стабилизированы.
Тем не менее, числа

являются компонентами кватерниона

, который переводит орт

в вектор

в результате преобразования

, где звездочка означает сопряжение кватерниона, а кружочек -- кватернионное умножение. Вместо

можно было бы и другой орт выбрать. Но даже выбрав орт, можно увидеть, что кватернион таким образом определяется неоднозначно, появляется одна степень свободы. Среди решений уравнения

имеется кватернион поворота по большому кругу

где скалярная часть кватерниона равна нулю и

Можно обнаружить, что существуют и решения с ненулевой скалярной частью:

для любого

тоже является решением.
Кстати, если выбрать

и рассмотреть преобразование вектора

в вектор

, то видно, что такой поворот должен осуществляться однозначно на угол

вокруг оси с направлением

. Это еще одно пояснение, чисто геометрическое, объясняющее появление двойки в выражениях. Таким образом, и в плоском, и в пространственном случае решается "квадратное" уравнение

на компоненты кватерниона, а в плоском случае это то же самое, что решать уравнение

относительно

.
С помощью преобразований Леви-Чивиты и Кустаанхеймо-Штифеля мы описываем движение космического аппарата не с помощью непрерывного множества параметризованных временем декартовых координат, а с помощью непрерывного множества поворотов-растяжений пространства, которые также параметризуются временем (правда, фиктивным).



