Вот это уравнение легкое но решается долго.

в целых числах.
Умножим обе части уравнения на (х). Получим:




Допустим, что существуют целые положительные

корни. В исходное уравнение подставим фиксированный корень
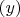
(который по предположению существует) и будем искать соответствующий именно ему

. Соответствовать может только один положительный, один отрицательный, два комплексных корня

. Другого расклада быть не может. Пара

, приведённая
Deggial в качестве контрпримера (наличия бесконечного количества комплексных корней), не подходит, т.к. переменная
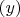
по предположению целая и фиксированна. А, уравнение четвёртой степени при фиксированном (у) не может иметь более четырёх корней. Вероятно,
Deggial, что-то не понял или я плохо объяснила. Может, я что-то не понимаю. Но, что?
Тогда возможны два случая:
1).

оба комплексные

2).

оба действительные

Очевидным является факт, что, если в исходном уравнении существует хотя бы один из ненулевых корней (+целый корень х;-целый корень х)при целом ненулевом корне (у), то

,

,

целое. Тогда

Получили, что (

) целое ненулевое число. Такое возможно?