Критерий секвенциальной непрерывности линейного функционала

[red_alert]

Известен следующий критерий: линейный функционал над ТВП непрерывен тогда и только тогда, когда его ядро замкнуто. Необходимость очевидна, доказательство достаточности следующее:

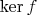
Пусть $f$ - линейный функционал над $X$ и $\ker f$ замкнуто. Считая, что $f \ne 0$ (иначе все очевидно), возьмем $x \in X \setminus \ker f$. Так как $X \setminus \ker f$ открыто, то в $X \setminus \ker f - x$ лежит некоторая окрестность нуля $U$, которую (в силу свойств ТВП) можно считать уравновешенной. Тогда и $f(U)$ уравновешено. Предположим, что $f(U)$ неограничено, тогда $f(U) = \mathbb{R}$ и $\exists y \in U: f(y) = -f(x)$. Но тогда $x + y \in \ker f$ - противоречие. Значит, $f(U)$ ограничено, то есть $\exists C > 0: U \subset \{x \in X: f(x) \le C\}$. Поэтому последнее множество - окрестность нуля, а вместе с тем и $\forall \varepsilon > 0\;\{x \in X: f(x) \le \varepsilon\}$ - окрестность нуля. Из последнего очевидно, что $f$ переводит направленность, сходящуюся к нулю, в направленность, сходящуюся к нулю.

Верен ли аналог этого критерия: линейный функционал над ТВП секвенциально непрерывен тогда и только тогда, когда его ядро секвенциально замкнуто?

Доказательство можно было бы повторить, заменив "открытость", "замкнутость", "окрестность" и "направленность" на соответственно "секвенциальную открытость", "секвенциальную замкнутость", "секвенциальную окрестность" и "последовательность", если бы удалось доказать, что любая секвенциальная окрестность нуля содержит уравновешенную секвенциальную подокрестность. Подозреваю, что на самом деле это неверно, но контрпример придумать не могу.

[Oleg Zubelevich]

red_alert в сообщении #987913 писал(а):

секвенциальная окрестность нуля

а это ччто такое?

[red_alert]

$U$ - секвенциальная окрестность точки $x$, если любая последовательность, сходящаяся к $x$, содержится в $U$, начиная с некоторого индекса.

[Slow]

red_alert в сообщении #987921 писал(а):

$U$ - секвенциальная окрестность точки $x$, если любая последовательность, сходящаяся к $x$, содержится в $U$, начиная с некоторого индекса.

Чем тогда отличается секвенциальная окрестность от обычной окрестности?

[red_alert]

Тем, что сходящаяся направленность не обязана в ней начиная с некоторого индекса содержаться. Обратное, конечно, верно: каждая окрестность является секвенциальной окрестностью.

[AGu]

Похоже, что ответ положительный: см. [1], стр. 47, теорема 1.4.7.
(Прошу проверить, я не вчитывался.)

[1] Thomas Beatty. Sequential topologies and their application to a new class of locally convex spaces. Florida Atlantic University, 1993.

Это первое, что нагуглилось. Возможно, есть и более удобные ссылки.

[red_alert]

Да, это то, что надо. Спасибо. Правда, там дополнительно предполагается (и используется) хаусдорфовость пространства, которая в первом критерии была вроде бы не нужна...

upd: хотя на самом деле и не хаусдорфовость используется, а "секвенциальная хаусдорфовость" - единственность предела последовательностей (а не направленностей).

[red_alert]

В книге предлагается следующая идея: вместе с исходной топологией рассматривать "ассоциированную", порожденную всеми секвенциально открытыми множествами. Секвенциальная замкнутость/непрерывность в исходной топологии - это замкнутость/непрерывность в ассоциированной. Если бы удалось доказать, что ассоциированная с векторной топологией тоже векторная, то новый критерий можно было бы напрямую получить из старого (таким образом, избавиться и от требования хаусдорфовости). Скорее всего, это неверно (раз не доказывается). Как можно было бы это показать?

[AGu]

red_alert в сообщении #988336 писал(а):

хотя на самом деле и не хаусдорфовость используется, а "секвенциальная хаусдорфовость" - единственность предела последовательностей (а не направленностей).

Эта «секвенциальная хаусдорфовость» в общем случае занимает промежуточное положение между $T_1$ и $T_2$, но в равномеризуемом случае (в частности, в случае ТВП) отделимости $T_0$, $T_1$ и $T_2$ равносильны, а значит, «секвенциальная хаусдорфовость» ТВП равносильна хаусдорфовости.

[red_alert]

red_alert в сообщении #988655 писал(а):

В книге предлагается следующая идея: вместе с исходной топологией рассматривать "ассоциированную", порожденную всеми секвенциально открытыми множествами. Секвенциальная замкнутость/непрерывность в исходной топологии - это замкнутость/непрерывность в ассоциированной. Если бы удалось доказать, что ассоциированная с векторной топологией тоже векторная, то новый критерий можно было бы напрямую получить из старого (таким образом, избавиться и от требования хаусдорфовости). Скорее всего, это неверно (раз не доказывается). Как можно было бы это показать?

Да, это неверно: R. M. Dudley. On Sequential Convergence, стр. 495, теорема 6.6 и замечания после нее.

[red_alert]

Оказалось, что критерий все же верен и без предположения хаусдорфости.
Доказательство: Zhang Zhi-yao. Characterization of Mazur spaces, стр. 309.
Там предполагается локальная выпуклость пространства, но по сути она не используется.

[AGu]

red_alert в сообщении #992460 писал(а):

Доказательство: Zhang Zhi-yao. Characterization of Mazur spaces, стр. 309.

Спасибо. Симпатичное доказательство.

(Оффтоп)

Ну и журнальчик! Безобразный набор, ужасный английский.