Деньги под стартап дают тогда, когда у него имеется хотя бы прототип устройства. У Вас есть прототип гипотезы? Числа там какие-нибудь посчитать, проверить в простом случае, например...
Я решил подсчитать количество четырехугольников в нашем многоугольнике из

вершин, для этого перенумеровал вершины многоугольника и попробовал понять сколько можно получить четырехугольников из n вершин. Оказалось, что можно подсчитать число
сочетаний из

по

(потому что нас интересуют четырехугольники), и оно и будет количеством всевозможных четырехугольников в нашем n - угольнике. Проверил для

и

, сошлось, для

, имеем

пересечений, для

, имеем
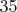
пересечений. Сейчас хочу доказать, что количество четырехугольников

количеству пересечений. Пойду думать дальше. Спасибо за подсказки
 -- 17.02.2015, 15:45 --
-- 17.02.2015, 15:45 --Факт, конечно, очень простой, но его всё-таки надо доказать честно.

Пусть n - чётное число, следовательно

- нечётное (1)

, т.к.



для всех

удовлетворяющих условию (1)
Так можно доказать?



