8 сделайте, она простая, и понять её условие просто; проблема в том, что ещё проще его понять неправильно.
Потому и утонули, что нарисовали. Семиугольник -- это слишком мало и, соответственно, слишком сложно. Берите лучше энугольник, а ещё лучше -- эм. А потом прикиньте: каждая пара пересекающихся диагоналей -- это сколько разных вершин?...
(ну и потом ещё чуть-чуть)
Я знаю формулу по которой можно подсчитать количество диагоналей зная количество вершин -

. Далее зная количество диагоналей, я могу подсчитать сколько пересечений образуется в "первом уровне" (на рисунках я отметил красным и синим цветами). Но дальше сложнее...
Для

имеем

диагоналей и

пересечений. На "последнем уровне" образуется треугольник.

Для

имеем

диагоналей и
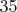
пересечений. На "последнем уровне" образуется "звездочка" (четырнадцать пересечений).




