Вышло нечто такое:
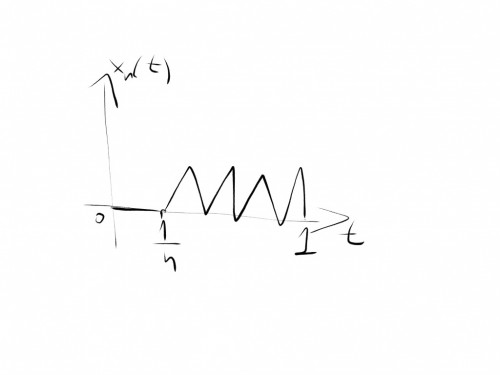
Значения в точках

равны нулю, а между ними такие "горочки" с достаточно малым значением в вершине(значение зависит от номера горочки) - чтобы величина

убегала в ноль. Тогда последовательность, очевидно, фундаментальна. Но предельный элемент обязан обладать свойствами: нулевые значения в точках последовательности

и положительная производная между соседними точками этой последовательности, а значит, в любой окрестности нуля у него будут положительные значения. Ну и не забыть "сгладить" последовательность в вершинах для непрерывной дифференцируемости.