Во-первых, от констант можно избавиться, вернувшись на шаг назад, и расставив пределы интегрирования, как я вам уже говорил.
Во-вторых, есть другой способ, как вам сказал
Alex-Yu. Для начала, надо понимать, что справа и слева у вас разные константы. Обозначим их, например, как

и
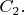
Дальше, вы должны записать окончательную формулу, удерживая эти константы. У вас получится какое-то решение, но не до конца ещё определённое, а зависящее от этих констант. Пусть это будет какая-то функция

А дальше вы должны записать начальные условия. Например, вы знаете, что в начальный момент времени

у вас тёк ток

Значит, вы должны записать условие:

Хорошо. Но это пока только одно уравнение. А констант у вас две. Но вы можете подставить это

в выражение для цепи - в дифференциальное уравнение:

- и получить отсюда значение производной в начальный момент:

Теперь и его можно использовать для записи условия:

И вот теперь, у вас есть два уравнения, и две неизвестных:

и
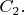
И решая эту систему уравнений, вы можете эти неизвестные найти - зафиксировать константы. И подставив их, получить окончательную формулу переходного процесса.



