Компактная укладка ромбододекаэдров

[kavict]

Задача:
Имеется $N$ одинаковых ромбододекаэдров (как известно, это параллелоэдр). Требуется уложить их так, чтобы сфера, содержащая эту укладку, была минимального радиуса (назовем такую укладку компактной).

Предлагаемый алгоритм укладки:
Складываем гранями два ромбододекаэдра. Эта укладка из двух тел по определению является компактной. Третий элемент добавляем в том месте, где его центр располагается наиболее близко к центру объема множества из двух элементов:

Следующий элемент добавляем так же - туда, где его центр располагается наиболее близко к общему центру уже уложенных трех элементов:
, и т.д.

Как доказать, что этот алгоритм приводит (или не приводит) к компактной укладке произвольного числа многогранников?

[grizzly]

Поскольку такая укладка заполняет пространство без пропусков и наложений, то, конечно, она в пределе будет компактной (в Вашем понимании термина).

Для небольших значений $N$ эта укладка не обязательно будет оптимальной. При $N=5$ это видно невооружённым глазом -- видно же, что первые два выгодно раздвинуть и в образовавшееся пространство втиснуть уголки остальных трёх. Радиус сферы, естественно, станет меньше.

Посмотрите здесь, как это происходит с укладками других фигур / тел в зависимости от $N$.

[ИСН]

Ну они же укладываются, не оставив свободного места? Значит, компактнее некуда.
Или вопрос в чём-то другом - например, в возможности продолжения этой укладки?

[kavict]

grizzly в сообщении #972566 писал(а):

Поскольку такая укладка заполняет пространство без пропусков и наложений, то, конечно, она в пределе будет компактной (в Вашем понимании термина).

Извините, не понял - в каком пределе?

[ИСН]

В пределе $N\to\infty$.

[grizzly]

kavict в сообщении #972577 писал(а):

в каком пределе?

Начиная с некоторого $N_0$ такая укладка будет оптимальной для любого количества $N>N_0$ ромбододекаэдров.

[kavict]

ИСН в сообщении #972567 писал(а):

Ну они же укладываются, не оставив свободного места? Значит, компактнее некуда.
Или вопрос в чём-то другом - например, в возможности продолжения этой укладки?

То, что многогранники укладываются так, что не остается свободного места между ними, еще не означает компактности укладки в указанном выше смысле. Вопрос состоит в том, обеспечивает ли описанный алгоритм такую укладку заданного числа $N$ ромбододекаэдров ($N>5$), что радиус описанной сферы будет минимально возможным, и никакая перестановка внешнего элемента укладки не уменьшит этот радиус.

[grizzly]

kavict в сообщении #972587 писал(а):

Вопрос состоит в том, обеспечивает ли описанный алгоритм такую укладку заданного числа $N$ ромбододекаэдров ($N>5$), что радиус описанной сферы будет минимально возможным, и никакая перестановка внешнего элемента укладки не уменьшит этот радиус.

Очевидно, не обеспечивает. Поверьте, что $N_0$ намного больше 5. Если Вам достанет пространственного воображения, то для $N=7$ Вы сможете представить, что предложенная укладка не будет оптимальной.

Насколько я понимаю, Вас интересует вопрос: можно ли найти $N_0$ и доказать минимальность этого $N_0$ аналитически? Очень сомневаюсь. Я прошу Вас пройти по предложенной ссылке и убедиться, что подобные, но значительно более простые вопросы на плоскости решаются вычислительными методами в поиске рекордов (а не доказательств).

[grizzly]

kavict
У меня закрались сомнения, что и при сколь угодно больших $N$ в некоторых случаях можно будет произвести шевеления Вашей конфигурации, позволяющее уменьшить радиус сферы. Представьте себе укладку, идеально заполняющую объём шара; тогда добавление ещё одного тела резко увеличивает необходимый радиус. Здесь я не уверен.

[kavict]

grizzly в сообщении #972590 писал(а):

kavict в сообщении #972587 писал(а):

Вопрос состоит в том, обеспечивает ли описанный алгоритм такую укладку заданного числа $N$ ромбододекаэдров ($N>5$), что радиус описанной сферы будет минимально возможным, и никакая перестановка внешнего элемента укладки не уменьшит этот радиус.

Очевидно, не обеспечивает. Поверьте, что $N_0$ намного больше 5. Если Вам достанет пространственного воображения, то для $N=7$ Вы сможете представить, что предложенная укладка не будет оптимальной.

Вот укладка для $N=7$, построенная по описанному алгоритму:
, и она же - с другой стороны:
Как, по Вашему, нужно переставить любой элемент, чтобы радиус описанной сферы уменьшился?

[grizzly]

kavict в сообщении #972630 писал(а):

Как, по Вашему, нужно переставить любой элемент, чтобы радиус описанной сферы уменьшился?

Боюсь, я не смогу изобразить это такими же красивыми рисунками. Я попробую на словах. Только я буду отталкиваться от самого первого из Ваших рисунков в этой теме. Давайте присвоим буквы обозначенным там телам. Первые 2 по алгоритму -- это Л(левый) и П(правый). Последующие -- В(верхний), Н(нижний), Д(дальний), Б(ближний); здесь если и спутаем пары, то это не критично.

Ниже все числа даны приближённо, на глаз, и нужны только чтоб не сбиться в пути.
Длина стороны ромба = 1.
Диаметр конфигурации в направлении Д--Б = 5.2.
Диаметр конфигурации в направлении П--Л = 3.2.
Диаметр обрамляющей сферы -- 5.4.
Раздвинем П и Л симметрично в направлениях П--Л на 1 ед. (по 0.5 каждый от центра). Это движение не увеличит диаметр обрамляющей сферы.
Д и Б будем отодвигать вместе с Л; В и Н -- вместе с П.
Очевидно, что Д, Б, В и Н могут быть немного задвинуты в образовавшийся в центре просвет. Такое задвижение уменьшит радиус конфигурации. Но мы не будем задвигать их максимально плотно -- оставим небольшой зазор для Седьмого тела.

Поправьте меня, если я ошибся.

[ИСН]

grizzly, Ваше изложение уподоблю подлодке, плавающей на боку.
Очевидно, в этой конфигурации у нас есть один уникальный шарик, касающийся только трёх других (у остальных - больше). Далее есть три, касающиеся его, а потом ещё три остальных. Так вот, немного раздвинем в стороны первые три (там есть место, потому что они не упирались в сферу), и это даст нам возможность вдвинуть уникальный немножко глубже между ними; это и будет ответ.

-- менее минуты назад --

А так я согласен, что никакого $N_0$, скорее всего, нет. Плотнейшая упаковка хоть и будет доминировать, но не абсолютно, а в каком-то другом смысле.

[grizzly]

ИСН
Согласен и спасибо за помощь. Моё пространственное воображение оставляет желать и желать.

[kavict]

Мне кажется, мы говорим о разном. Наверное, я плохо сформулировал суть вопроса. Попробую еще раз.
Допустим, у нас имеется 7 одинаковых ромбододекаэдров. Будем складывать их во всевозможные комбинации, как, например, показано на рисунке:

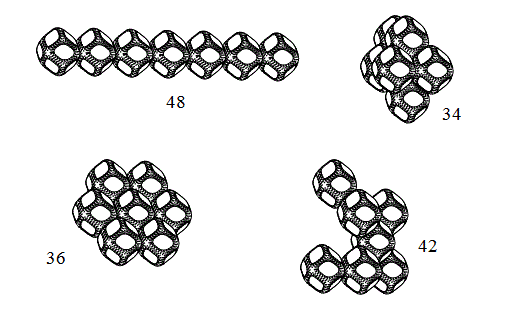
(числа, стоящие рядом с каждой конфигурацией, к данному вопросу отношения не имеют)
Представим, что вокруг каждой конфигурации описана сфера, и радиус этих сфер, очевидно, будет различным. Например, у конфигурации, обозначенной числом 48 описанная сфера будет наибольшего радиуса, а у обозначенной числом 34 - наименьшая из четырех показанных.
Перепробывав всевозможные варианты взаимного расположения этих семи ромбододекаэдров, найдем тот, у которого радиус описанной сферы будет наименьшим - обозначим эту конфигурацию $K_7$. Это значит, что семь ромбододекаэдров данного размера никак нельзя уместить в меньшую сферу.
Теперь возьмем 8 таких же ромбододекаэдров и будем их складывать в различных комбинациях до тех пор, пока не найдем такую, у которой радиус описанной сферы будет наименьшим для восьми ромбододекаэдров - обозначим эту укладку $K_8$. В моей терминологии $K_7$ и $K_8$ - компактные укладки.
Вопрос: будет ли укладка $K_8$ отличаться от $K_7$ только добавлением одного элемента, или это будут совсем разные укладки?
У меня по компьютерным моделям получается, каждая последующая компактная укладка получается из предыдущей добавлением нового элемента, т.е., чтобы получить $K_8$, нужно к $K_7$ добавить новый элемент в определенном месте, как описано в алгоритме.

[ИСН]

В Ваших комбинациях набор возможных положений дискретен? То есть ромбододекаэдры обязательно должны быть слеплены по граням?