gammaker1)Во первых, зачем вы написали обратное п.ф (ещё и коэффициенты куда то засунули)? Граничные условия можно найти просто применив к ним п.ф.
2)Но вот например,
![$\[\theta (x)\]$ $\[\theta (x)\]$](https://dxdy-04.korotkov.co.uk/f/3/b/f/3bf9cce9bc7281bbedd24da762a72e1682.png)
- это же функция Хевисайда? Ну так и найдите её образ фурье!
3)Просто тупо возьмите уже п.ф. по
![$\[x\]$ $\[x\]$](https://dxdy-01.korotkov.co.uk/f/c/a/6/ca64a19efa21fcdb6a66b9cc0f37208982.png)
от
![$\[{\nabla ^2}u = 0\]$ $\[{\nabla ^2}u = 0\]$](https://dxdy-01.korotkov.co.uk/f/c/2/7/c27a89b9e0936ff241c133db4afa4e7782.png)
. Какой вид приобретёт уравнение? Вы знаете хотя бы для функции одной переменной, если
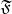
![$\[(f)\]$ $\[(f)\]$](https://dxdy-04.korotkov.co.uk/f/b/5/5/b55884d7f3e8b3218d768a1f7c61d62982.png)
![$\[ = \hat f\]$ $\[ = \hat f\]$](https://dxdy-01.korotkov.co.uk/f/8/d/b/8db8ed795ce5100a0796b4f0627f8cde82.png)
, то чему будет равно
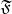
![$\[(\frac{{df}}{{dx}})\]$ $\[(\frac{{df}}{{dx}})\]$](https://dxdy-01.korotkov.co.uk/f/8/4/8/84876b369a0888b64ee00da6f4161d1082.png)
1) Коэффициенты поправил. А почему нужно прямое, а не обратное? Мы ведь переходим от

к

, а не наоборот. Хотя вроде всё равно то же самое получается.
2) Точно! А я голову ломал, что это за функция! В итоге решил, что это просто какая-то неизвестная функция в общем виде. Просто у нас в институте функцию Хевисайда другой буквой обозначают, а в этом задачнике, оказывается, так.
-- 20.01.2015, 14:27 --Получается расходящийся интеграл.




